
【题目】如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
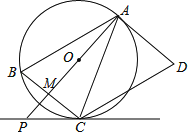
(1)求证:∠BAP=∠CAP;
(2)判断直线PC与⊙O的位置关系,并说明理由;
(3)若AB=5![]() ,BC=10,求PC的长.
,BC=10,求PC的长.
【答案】(1)见解析;(2)PC与圆O相切,理由见解析;(3)![]()
【解析】
(1)过C点作直径CE,连接EB,由CE为直径得∠E+∠BCE=90°,由AB∥DC得∠ACD=∠BAC,而∠BAC=∠E,∠BCP=∠ACD,所以∠E=∠BCP,于是∠BCP+∠BCE=90°,然后根据切线的判断得到结论;
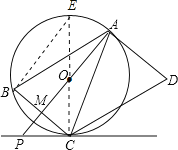
(2)根据切线的性质得到OA⊥AD,而BC∥AD,则AM⊥BC,根据垂径定理有BM=CM=![]() BC=5,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM的长度,设⊙O的半径为r,则OC=r,OM=AM-r=5
BC=5,根据等腰三角形性质有AC=AB=9,在Rt△AMC中根据勾股定理计算出AM的长度,设⊙O的半径为r,则OC=r,OM=AM-r=5![]() -r,在Rt△OCM中,根据勾股定理计算出r=3
-r,在Rt△OCM中,根据勾股定理计算出r=3![]() ,由CE=2r,利用中位线性质得BE的长度,然后判断Rt△PCM∽Rt△CEB,根据相似比可计算出PC.
,由CE=2r,利用中位线性质得BE的长度,然后判断Rt△PCM∽Rt△CEB,根据相似比可计算出PC.
(1)证明:∵AD是⊙O的切线,
∴OA⊥AD,
∵BC∥AD,
∴OA⊥BC,
∴弧BE=弧CF,
∴∠BAP=∠CAP;
(2)PC与圆O相切,理由为:
过C点作直径CE,连接EB,如图,
∵CE为直径,
∴∠EBC=90°,即∠E+∠BCE=90°,
∵AB∥DC,
∴∠ACD=∠BAC,
∵∠BAC=∠E,∠BCP=∠ACD.
∴∠E=∠BCP,
∴∠BCP+∠BCE=90°,即∠PCE=90°,
∴CE⊥PC,
∴PC与圆O相切;
(2)∵AD是⊙O的切线,切点为A,
∴OA⊥AD,
∵BC∥AD,
∴AM⊥BC,
∴BM=CM=![]() BC=5,
BC=5,
∴AC=AB=5![]() ,
,
在Rt△AMC中,AM=![]() =5
=5![]() ,
,
设⊙O的半径为r,则OC=r,OM=AM﹣r=5![]() ﹣r,
﹣r,
在Rt△OCM中,OM2+CM2=OC2,即![]() +52=r2,
+52=r2,
解得:r=3![]() ;
;
∴CE=2r=6![]() ,OM=5
,OM=5![]() ﹣r=2
﹣r=2![]() ,
,
∴BE=2OM=4![]() ,
,
∵∠E=∠MCP,
∴Rt△PCM∽Rt△CEB,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∴PC=![]() .
.


 小学教材全测系列答案
小学教材全测系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图,对于下列说法:①abc<0;②a﹣b+c<0;③3a+c<0;④当﹣1<x<3时,y>0.其中正确的是( )
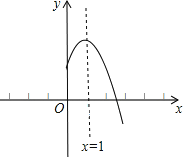
A.①②B.①③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图示,在平面直角坐标系中,二次函数![]() (
(![]() )交
)交![]() 轴于
轴于![]() ,
,![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
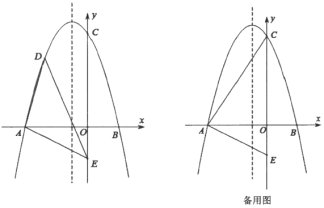
(1)求二次函数的表达式;
(2)点![]() 是第二象限内的点抛物线上一动点
是第二象限内的点抛物线上一动点
①求![]() 面积最大值并写出此时点
面积最大值并写出此时点![]() 的坐标;
的坐标;
②若![]() ,求此时点
,求此时点![]() 坐标;
坐标;
(3)连接![]() ,点
,点![]() 是线段
是线段![]() 上的动点.连接
上的动点.连接![]() ,把线段
,把线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,点
,点![]() 是点
是点![]() 的对应点.当动点
的对应点.当动点![]() 从点
从点![]() 运动到点
运动到点![]() ,则动点
,则动点![]() 所经过的路径长等于______(直接写出答案)
所经过的路径长等于______(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
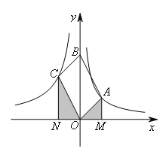
【题目】如图,OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限内的点C分别在双曲线![]() 和
和![]() 的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:
①阴影部分的面积为![]() ;
;
②若B点坐标为(0,6),A点坐标为(2,2),则![]() ;
;
③当∠AOC=![]() 时,
时,![]() ;
;
④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是 ____________(填写正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“打开电视剧,正在播足球赛”是必然事件
B.甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
C.一组数据2,4,5,5,3,6的众数和中位数都是5
D.“掷一枚硬币正面朝上的概率是![]() ”表示每抛硬币2次就有1次正面朝上
”表示每抛硬币2次就有1次正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球试验,每次摸出一个球,放回、搅匀,下表是活动进行中的一组统计数据,
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.230 | 0.231 | 0.300 | 0.260 | 0.254 |
袋中白球的个数约为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
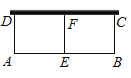
【题目】某扶贫单位为了提高贫困户的经济收入,购买了33m的铁栅栏,准备用这些铁栅栏为贫困户靠墙(墙长15m)围建一个中间带有铁栅栏的矩形养鸡场(如图所示).
(1)若要建的矩形养鸡场面积为90m2,求鸡场的长(AB)和宽(BC);
(2)该扶贫单位想要建一个100m2的矩形养鸡场,请直接回答:这一想法能实现吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是⊙O的直径,AM、BN是⊙O的两条切线,D、C分别在AM、BN上,DC切⊙O于点E,连接OD、OC、BE、AE,BE与OC相交于点P,AE与OD相交于点Q,已知AD=4,BC=9,以下结论:
①⊙O的半径为![]() ,②OD∥BE ,③PB=
,②OD∥BE ,③PB=![]() , ④tan∠CEP=
, ④tan∠CEP=![]()
其中正确结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面上,对于给定的线段AB和点C,若平面上的点P(可以与点C重合)满足,∠APB=∠ACB.则称点P为点C关于直线AB的联络点.

在平面直角坐标系xOy中,已知点A(2,0),B(0,2),C(﹣2,0).
(1)在P1(2,2),P(1,0),R(1+![]() ,1)三个点中,是点O关于线段AB的联络点的是 .
,1)三个点中,是点O关于线段AB的联络点的是 .
(2)若点P既是点O关于线段AB的联络点,同时又是点B关于线段OA的联络点,求点P的横坐标m的取值范围;
(3)直线y=x+b(b>0)与x轴,y轴分交于点M,N,若在线段BC上存在点N关于线段OM的联络点,直接写出b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com