

分析 (1)由长方形的性质得出AB=DC,AD=BC,由题意得出AB=DC=2,即可得出D点的坐标;
(2)设∠BEO=2x,则∠EOX=2x,作FG∥OX,得出∠FOX=$\frac{1}{2}$∠BOY+∠BOE+∠EOX=$\frac{1}{2}$∠BOY+n+2x,由角平分线得出$\frac{1}{2}$∠BOY=$\frac{1}{2}$(90°-n+2x),得出∠FOX=45°+$\frac{1}{2}$n+x,由平行线得出∠EFG=∠BEF=x,得出∠OFG=180°-∠FOX=135°-$\frac{1}{2}$n-x,即可得出∠OFE的度数;
(3)作AM⊥y轴于M,先求出矩形ABCD的面积,△OBD的面积=△ODM的面积-△ABD的面积-梯形AMOB的面积,得出方程,解方程即可求出t的值.
解答 解:(1)∵四边形ABCD是长方形,
∴AB=DC,AD=BC,
∵点A(1,8),B(1,6),C(7,6),
∴AB=DC=2,
∴D点的坐标为:(7,8);
故答案为:(7,8);
(2)∵∠BOY的平分线和∠BEO的平分线交于点F,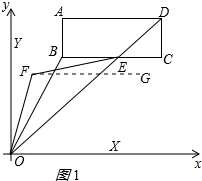 ∴∠BOF=∠FOY=$\frac{1}{2}$∠BOY,∠BEF=∠OEF=$\frac{1}{2}$∠BEO,
∴∠BOF=∠FOY=$\frac{1}{2}$∠BOY,∠BEF=∠OEF=$\frac{1}{2}$∠BEO,
∵BC∥OX,
∴∠BEO=∠EOX,
设∠BEO=2x,
则∠EOX=2x,
作FG∥OX,如图1所示:
则∠FOX=$\frac{1}{2}$∠BOY+∠BOE+∠EOX=$\frac{1}{2}$∠BOY+n+2x,
又∵$\frac{1}{2}$∠BOY=$\frac{1}{2}$(90°-n+2x)=45°-$\frac{1}{2}$n-x,
∴∠FOX=45°-$\frac{1}{2}$n-x+n+2x=45°+$\frac{1}{2}$n+x,
∵BC∥FG∥OX,
∴∠EFG=∠BEF=x,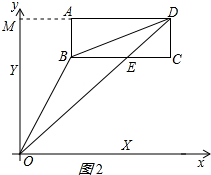 ∴∠OFG=180°-∠FOX=135°-$\frac{1}{2}$n-x,
∴∠OFG=180°-∠FOX=135°-$\frac{1}{2}$n-x,
∴∠OFE=∠EFG+∠OFG=135°-$\frac{1}{2}$n;
(3)存在某一时刻,使△OBD的面积等于长方形ABCD面积的$\frac{2}{3}$,t=2;理由如下:
作AM⊥y轴于M,如图2所示:
∵S矩形ABCD=2×6=12,
S△OBD=S△ODM-S△ABD-S梯形AMOB=12×$\frac{2}{3}$,
∴$\frac{1}{2}$×(8-$\frac{3}{2}$t)×7-$\frac{1}{2}$×12-$\frac{1}{2}$(2+8-$\frac{3}{2}$t)×1=12×$\frac{2}{3}$,
解得:t=2.
点评 本题是四边形综合题目,考查了矩形的性质、坐标与图形性质、角的平分线、平行线的性质、三角形内角和定理、图形面积的计算等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线才能得出结果.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
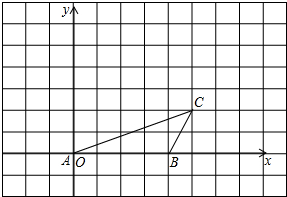
 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com