
 如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).分析 (1)过点A作AM⊥EF于点M,过点C作CN⊥EF于点N.设CN=x,分别表示出EM、AM的长度,然后在Rt△AEM中,根据tan∠EAM=$\frac{\sqrt{3}}{3}$,代入求解即可;
(2)根据(1)求得的结果,可得EF=DF+CD,代入求解.
解答 解:(1)过点A作AM⊥EF于点M,过点C作CN⊥EF于点N,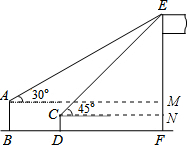 设CN=x,
设CN=x,
在Rt△ECN中,
∵∠ECN=45°,
∴EN=CN=x,
∴EM=x+0.7-1.7=x-1,
∵BD=5,
∴AM=BF=5+x,
在Rt△AEM中,
∵∠EAM=30°
∴$\frac{EM}{AM}$=$\frac{\sqrt{3}}{3}$,
∴x-1=$\frac{\sqrt{3}}{3}$(x+5),
解得:x=4+3$\sqrt{3}$,
即DF=(4+3$\sqrt{3}$)(米);
(2)由(1)得:
EF=x+0.7=4+$3\sqrt{3}$+0.7
≈4+3×1.7+0.7
≈9.8≈10(米).
答:旗杆的高度约为10米.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据仰角构造直角三角形,利用三角函数的知识求解.


科目:初中数学 来源: 题型:填空题
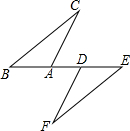 如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)
如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是BC=EF或∠BAC=∠EDF.(只填一个即可)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象在
如图,直线y=x-2与y轴交于点C,与x轴交于点B,与反比例函数y=$\frac{k}{x}$的图象在| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为36$\sqrt{3}$-54.
如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为36$\sqrt{3}$-54.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
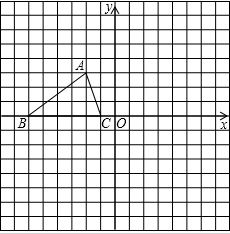 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com