Question

10．如图，∠AOB=30°，点M、N分别是射线OA、OB上的动点，OP平分∠AOB，且OP=6，当△PMN的周长取最小值时，四边形PMON的面积为36$\sqrt{3}$-54．

Answer 1

分析 设点P关于OA的对称点为C，关于OB的对称点为D，当点M、N在CD上时，△PMN的周长最小，此时△COD是等边三角形，求得三角形PMN和△COD的面积，根据四边形PMON的面积为：$\frac{1}{2}$（ S_△COD+S_△PMN）求得即可．

解答 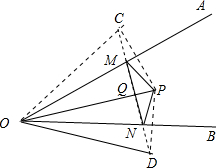解：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PC、PD．
∵点P关于OA的对称点为C，关于OB的对称点为D，
∴PM=CM，OP=OC，∠COA=∠POA；
∵点P关于OB的对称点为D，
∴PN=DN，OP=OD，∠DOB=∠POB，
∴OC=OD=OP=6，∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°，
∴△COD是等边三角形，
∴CD=OC=OD=6．
∵∠POC=∠POD，
∴OP⊥CD，
∴OQ=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$，
∴PQ=6-3$\sqrt{3}$
设MQ=x，则PM=CM=3-x，
∴（3-x）²-x²=（6-3$\sqrt{3}$）²，解得x=6$\sqrt{3}$-9，
∵S_△PMN=$\frac{1}{2}$MN×PQ，
S_△MON=$\frac{1}{2}$MN×OQ，
∴S_{四边形PMON}=S_△MON+S_△PMN=$\frac{1}{2}$MN×PQ+$\frac{1}{2}$MN×OQ=$\frac{1}{2}$MN×OP=$\frac{1}{2}$×（6$\sqrt{3}$-9）×6=36$\sqrt{3}$-54．
故答案为36$\sqrt{3}$-54．

点评 此题主要考查轴对称--最短路线问题，熟知两点之间线段最短是解答此题的关键．