
分析 (1)首先设A种灯笼需x个,则B种灯笼个数=A种灯笼个数×$\frac{2}{3}$,根据关键语句“需采用A、B两种不同类型的灯笼500个”可列出一元一次方程,再解即可;
(2)购买A种灯笼所需费用+购买B种灯笼所需费用=所求费用.
解答 解:(1)设A种灯笼需x个,则B种灯笼个数为$\frac{2}{3}$x个,由题意得:
x+$\frac{2}{3}$x=500,
解得:x=300,
B种灯笼:300×$\frac{2}{3}$=200(个).
答:A种灯笼需300个、B种灯笼需200个.
(2)300×50+200×60
=15000+12000
=27000(元).
答:这次美化工程购置灯笼需27000元费用.
点评 此题主要考查了一元一次方程的应用,关键是正确理解题意,抓住题目中的关键语句,找出等量关系,列出方程.同时考查了总价=单价×数量的知识点.


科目:初中数学 来源: 题型:解答题
 如图所示,在离水面高度为5m的岸上C点有人用绳子拉船靠岸,开始时绳子CB与水面AB的夹角为30°,此人以每秒0.5m的速度往回收绳子,8s后船被拉到了点D的位置,问船向岸边移动了多少米?
如图所示,在离水面高度为5m的岸上C点有人用绳子拉船靠岸,开始时绳子CB与水面AB的夹角为30°,此人以每秒0.5m的速度往回收绳子,8s后船被拉到了点D的位置,问船向岸边移动了多少米?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 100(1+x)2=64 | B. | 100(1-x)2=64 | C. | 100(1-x2)=64 | D. | 100(1+x2)=64 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
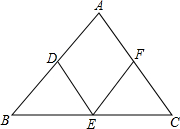 如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)
如图,在△ABC中,D、E、F分别是AB、BC、CA的中点,若添加一个条件,可以使四边形ADEF为菱形,你认为添加的条件可以是AB=AC.(只需要填写一个条件即可)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当AC=BD时,四边形ABCD是矩形 | |
| B. | 当AB=AD,CB=CD时,四边形ABCD是菱形 | |
| C. | 当AC=BD,AD=AB时,四边形ABCD是正方形 | |
| D. | 当AB=AD=BC时,四边形ABCD是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为乒乓球台横截面图,桌面长AB=280cm,球网MN=18cm,桌面距地面80cm,以BA的延长线上距A点20cm的O点为坐标原点,AB所在的直线为x轴,建立如图所示的坐标系.从O点抽出的球经过点C(50,$\frac{250}{9}$),且路径是抛物线的一部分,在距O点水平距离为150cm的地方,球达到最高点.
如图,为乒乓球台横截面图,桌面长AB=280cm,球网MN=18cm,桌面距地面80cm,以BA的延长线上距A点20cm的O点为坐标原点,AB所在的直线为x轴,建立如图所示的坐标系.从O点抽出的球经过点C(50,$\frac{250}{9}$),且路径是抛物线的一部分,在距O点水平距离为150cm的地方,球达到最高点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com