
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连接CE交AD于点F,连接BD交CE于点G,连接BE.下列结论中:
①CE=BD;
②△ADC是等腰直角三角形;
③∠ADB=∠AEB;
④CDAE=EFCG;
一定正确的结论有( )
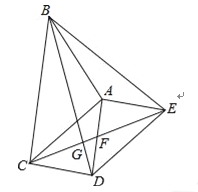
A.1个 B.2个 C.3个 D.4个
【答案】D
【解析】
试题分析:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即:∠BAD=∠CAE,
∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AE=AD,
∴△BAD≌△CAE(SAS),
∴CE=BD,
∴故①正确;
②∵四边形ACDE是平行四边形,
∴∠EAD=∠ADC=90°,AE=CD,
∵△ADE是等腰直角三角形,
∴AE=AD,
∴AD=CD,
∴△ADC是等腰直角三角形,
∴②正确;
③∵△ADC是等腰直角三角形,
∴∠CAD=45°,
∴∠BAD=90°+45°=135°,
∵∠EAD=∠BAC=90°,∠CAD=45°,
∴∠BAE=360°﹣90°﹣90°﹣45°=135°,
又AB=AB,AD=AE,
∴△BAE≌△BAD(SAS),
∴∠ADB=∠AEB;
故③正确;
④∵△BAD≌△CAE,△BAE≌△BAD,
∴△CAE≌△BAE,
∴∠BEA=∠CEA=∠BDA,
∵∠AEF+∠AFE=90°,
∴∠AFE+∠BEA=90°,
∵∠GFD=∠AFE,∠ADB=∠AEB,
∴∠ADB+∠GFD=90°,
∴∠CGD=90°,
∵∠FAE=90°,∠GCD=∠AEF,
∴△CGD∽△EAF,
∴![]() ,
,
∴CDAE=EFCG.
故④正确,
故正确的有4个.
故选:D.



科目:初中数学 来源: 题型:
【题目】如图,一个四边形花坛ABCD,被两条线段MN,EF分成四个部分,分别种上红、黄、紫、白四种花卉,种植面积依次是S1,S2,S3,S4,若MN∥AB∥CD,EF∥DA∥CB,则有( )
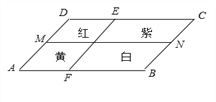
A. S1=S4 B. S1+S4=S2+S3 C. S1S4=S2S3 D. 都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部队将在指定山区进行军事演习,为了使道路便于部队重型车辆通过,部队工兵连接到抢修一段长3600米道路的任务,按原计划完成总任务的![]() 后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
后,为了让道路尽快投入使用,工兵连将工作效率提高了50%,一共用了10小时完成任务.
(1)按原计划完成总任务的![]() 时,已抢修道路 米;
时,已抢修道路 米;
(2)求原计划每小时抢修道路多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com