
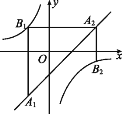
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为![]() (n为正整数).若
(n为正整数).若![]() ,则
,则![]() __,
__,![]() __.
__.
科目:初中数学 来源: 题型:
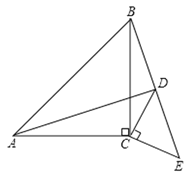
【题目】如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B,D,E在同一直线上,连接AD,BD.
(1)请探究AD与BD之间的位置关系并证明你的结论;
(2)若AC=BC=![]() ,DC=CE=
,DC=CE=![]() ,求线段AD的长;
,求线段AD的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球,1个绿球和n个白球,这些球除颜色外无其他差别.
(1)从袋中随机摸出一个球,记录其颜色,然后放回,搅匀,大量重复该实验,发现摸到绿球的频率稳定于0.2,求n的值;
(2)若![]() ,小明两次摸球(摸出一球后,不放回,再摸出一球),请用树状图画出小明摸球的所有结果,并求出两次摸出不同颜色球的概率.
,小明两次摸球(摸出一球后,不放回,再摸出一球),请用树状图画出小明摸球的所有结果,并求出两次摸出不同颜色球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究如图,在正方形![]() 中,点
中,点![]() 在
在![]() 边所在的直线上运动但不与点
边所在的直线上运动但不与点![]() 重合,点
重合,点![]() 在线段
在线段![]() .上运动,过点
.上运动,过点![]() 的直线
的直线![]() ,分别交
,分别交![]() 于点
于点![]() .
.
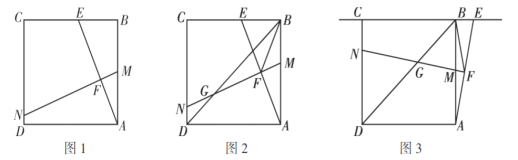
观察探究:(1)如图1,当点![]() 在边
在边![]() 上时,判断并说明
上时,判断并说明![]() 与
与![]() 的数量关系;
的数量关系;
探究发现:(2)勤奋小组在图1的基础上得到图2,点![]() 为
为![]() 中点时,其他条件不变,连接正方形的对角线
中点时,其他条件不变,连接正方形的对角线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,此时,
,此时,![]() ,请利用图2证明;
,请利用图2证明;
探究拓展:(3)如图3,缜密小组在勤奋小组的启发下,当点![]() 在点
在点![]() 右侧时,如果(2)中的其他条件不变,直线
右侧时,如果(2)中的其他条件不变,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,他们发现线段
,他们发现线段![]() 与
与![]() 之间存在数量关系,线段
之间存在数量关系,线段![]() 与
与![]() 之间也存在数量关系,请你直接写出.
之间也存在数量关系,请你直接写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=(x﹣m)(x﹣m﹣4)(m为常数).
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)求证:不论m为何值,该函数的图象的顶点纵坐标不变;
(3)若该函数的图象与x轴交点为A、B,与y轴交点为C,当﹣3≤m≤﹣1时,△ABC面积S的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点D是⊙O上的一点,点C是直径AB延长线上一点,连接BD,CD,且∠A=∠BDC.
(1)求证:直线CD是⊙O的切线;
(2)若CM平分∠ACD,且分别交AD,BD于点M,N,当DM=2时,求MN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点A在反比例函数y=﹣![]() 的图象上,点B、C都在反比例函数y=﹣
的图象上,点B、C都在反比例函数y=﹣![]() 的图象上,AB∥x轴,则点A的坐标为( )
的图象上,AB∥x轴,则点A的坐标为( )

A.(﹣![]() ,2
,2![]() )B.(﹣
)B.(﹣![]() ,
,![]() )C.(﹣
)C.(﹣![]() ,
,![]() )D.(﹣2
)D.(﹣2![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
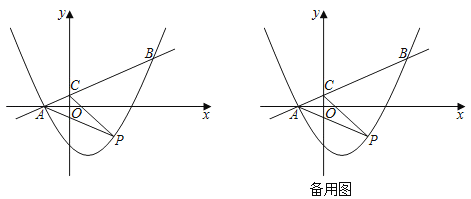
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+c与直线y=
x+c与直线y=![]() x+
x+![]() 交于A、B两点,已知点B的横坐标是4,直线y=
交于A、B两点,已知点B的横坐标是4,直线y=![]() x+
x+![]() 与x、y轴的交点分别为A、C,点P是抛物线上一动点.
与x、y轴的交点分别为A、C,点P是抛物线上一动点.
(1)求抛物线的解析式;
(2)若点P在直线y=![]() x+
x+![]() 下方,求△PAC的最大面积;
下方,求△PAC的最大面积;
(3)设M是抛物线对称轴上的一点,以点A、B、P、M为顶点的四边形能否成为平行四边形?若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
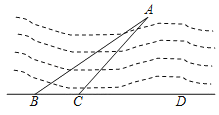
【题目】如图,为测量小岛A到公路BD的距离,先在点B处测得∠ABD=37°,再沿BD方向前进150m到达点C,测得∠ACD=45°,求小岛A到公路BD的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com