
分析 由已知条件得到$\frac{{x}^{2}+x+1}{x}$=$\frac{1}{a}$,利用分式的除法得x+1+$\frac{1}{x}$=$\frac{1}{a}$,即x+$\frac{1}{x}$=$\frac{1-a}{a}$,再表变形$\frac{{x}^{4}+{x}^{2}+1}{{x}^{2}}$得到x2+1+$\frac{1}{{x}^{2}}$,接着利用完全平方公式得到(x+$\frac{1}{x}$)2-1,所以$\frac{{x}^{4}+{x}^{2}+1}{{x}^{2}}$=$\frac{1-2a}{{a}^{2}}$,然后利用倒数定义即可得到原式的值.
解答 解:∵$\frac{x}{{x}^{2}+x+1}$=a,
∴$\frac{{x}^{2}+x+1}{x}$=$\frac{1}{a}$,
∴x+1+$\frac{1}{x}$=$\frac{1}{a}$,
∴x+$\frac{1}{x}$=$\frac{1-a}{a}$,
∴$\frac{{x}^{4}+{x}^{2}+1}{{x}^{2}}$=x2+1+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-1=($\frac{1-a}{a}$)2-1=$\frac{1-2a+{a}^{2}}{{a}^{2}}$-1=$\frac{1-2a}{{a}^{2}}$,
∴$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$=$\frac{{a}^{2}}{1-2a}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.本题的关键是利用倒数法求分式的值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
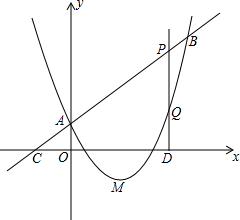 已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合).
已知:如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(2,-1),且与直线y=x+1相交于点A(0,1)和点B,P为线段AB上一动点(点P不与A、B重合).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
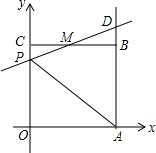 如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.
如图,已知正方形OABC的边长为2,顶点A、C分别在x、y轴的正半轴上,M是BC的中点.P(0,m)是线段OC上以一动点(C点除外).直线PM交AB的延长线于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com