
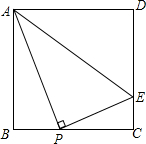
 如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.
如图,在正方形ABCD中,P是BC边上一点(不与点B,C重合),AP⊥PE.分析 (1)根据正方形的性质和已知条件证明∠PAB=∠EPC,即可证明:△ABP∽△PCF;
(2)根据△ABP∽△PCE,得到$\frac{AB}{PC}=\frac{AP}{PE}$=$\frac{PC}{CE}$,由已知条件得到BP=PC=$\frac{1}{2}$AB,于是得到$\frac{AB}{PC}=\frac{AP}{PE}$=$\frac{PC}{CE}$=2,由于∠APF=∠PCF=90°,于是得到△APE∽△PCE,由相似三角形的性质:对应边的比值相等即可证明FP2=FA•FC.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠B=∠PCD=90°,
∴∠PAB+∠APB=90°,
∵∠APE=90°,
∴∠EPC+∠APB=90°,
∴∠PAB=∠EPC,
∴△ABP∽△PCE;
(2)解:∵△ABP∽△PCE,
∴$\frac{AB}{PC}=\frac{AP}{PE}$=$\frac{PC}{CE}$,
∵P位于BC的中点,
∴BP=PC=$\frac{1}{2}$AB,
∴$\frac{AB}{PC}=\frac{AP}{PE}$=$\frac{PC}{CE}$=2,
∵∠C=∠APE=90°,
∴△APE∽△PCE,
∴$\frac{AE}{PE}=\frac{PE}{CE}$,
∴EP2=EA•EC.
点评 本题考查了正方形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
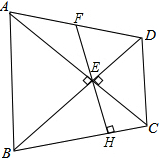 已知:△ABE和△DEC都是等腰直角三角形,∠AEB=∠DEC=90°,过E作EH⊥BC,交BC于H点,交AD于F点.当E是AC和BD的交点时,求证:
已知:△ABE和△DEC都是等腰直角三角形,∠AEB=∠DEC=90°,过E作EH⊥BC,交BC于H点,交AD于F点.当E是AC和BD的交点时,求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
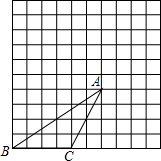 在如图所示10×10的方格中,有一个格点△ABC,请在图中画出两个格点△A1B1C1 和△A2B2C2,使△ABC∽△A1B1C1∽△A2B2C2(相似比不为1,且△A1B1C1为放大的三角形,△A2B2C2为缩小的三角形).
在如图所示10×10的方格中,有一个格点△ABC,请在图中画出两个格点△A1B1C1 和△A2B2C2,使△ABC∽△A1B1C1∽△A2B2C2(相似比不为1,且△A1B1C1为放大的三角形,△A2B2C2为缩小的三角形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
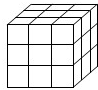 将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:
将一个正方体木块涂成红色,然后如图把它的棱三等分,再沿等分线把正方体切开,可以得到27个小正方体.观察并回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com