
| 时间x(天) | 每台空调的成本P(元) |
| 0<x≤5 | P=400 |
| 5<x≤12 | P=40x+200 |
分析 (1)分0<x≤5、5<x≤12,根据“总利润=单件利润×销售量”列出函数解析式;
(2)结合x的范围,分别根据一次函数和二次函数的增减性求解可得;
(3)先根据题意求得y1、P1,再由“厂家10天的销售利润与原计划的8天的销售利润持平”列方程求解可得.
解答 解:(1)当0<x≤5时,W=y(1400-P)=(2x+16)(1400-400)=2000x+16000;
当5<x≤12时,W=y(1400-P)=(2x+16)[1400-(40x+20)]=-80x2+1760x+19200.
(2)当0<x≤5时,W=2000x+16000,
∵2000>0,W随x的增大而增大,
∴当x=5时,W有最大值为26000元;
当5<x≤12时,W=-80x2+1760x+19200=-80(x-11)2+28880,
∴当x=11时,W有最大值28880元,
综上,第11天的利润最大,最大利润是28880元;
(3)y1=2×11+16=38件,P1=40×11+200=640元,
由题意得:[1400-640(1+a%)]×38×10=28880×8,
解得:a=23.75,
∴a的值为23.75.
点评 本题主要考查二次函数的应用及一元一次方程的应用,理解题意找到题目蕴含的相等关系是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
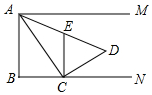 如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.
如图,射线AM平行于射线BN,∠B=90°,AB=4,C是射线BN上的一个动点,连接AC,作CD⊥AC,且AC=2CD,过C作CE⊥BN交AD于点E,设BC长为a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
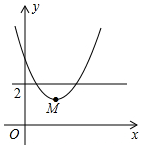 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )| A. | 0个或1个 | B. | 0个或2个 | C. | 1个或2个 | D. | 0个、1个或2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
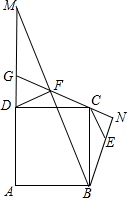 如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.
如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 中位数 | 众数 | 平均数 | 方差 |
| 9.2 | 9.3 | 9.1 | 0.3 |
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 方差 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com