
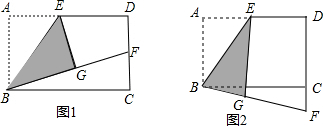
分析 (1)①只要证明Rt△EGF≌Rt△EDF即可;
②设DF=FC=a,则AB=BG=2a,GF=a,在Rt△BFC中,根据BF2=CF2+BC2列出方程即可解决问题.
(2)运用(1)中结论得出,△BEG∽△EFG,得$\frac{EG}{FG}$=$\frac{BG}{EG}$,推出EG2=BG•GF,设DC=AB=BG=a,则DF=FG=ka,推出EG2=ka2,推出EG=$\sqrt{k}$a,推出AD=2EG=2$\sqrt{k}$a,由此即可解决问题.
解答 解:(1)①证明:如图1中,连接EF.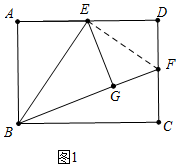
∵矩形ABCD中,E是AD的中点,△ABE沿BE折叠后得到△GBE,
∴AE=DE,AE=EG,∠A=∠BGE=∠D=90°,
在Rt△EFG和Rt△EFG中,
$\left\{\begin{array}{l}{EF=EF}\\{EG=ED}\end{array}\right.$,
∴Rt△EGF≌Rt△EDF,
∴FG=DF;
②设DF=FC=a,则AB=BG=2a,GF=a,
在Rt△BFC中,∵BF2=CF2+BC2,
∴(3a)2+a2=42,
解得a=$\frac{2\sqrt{5}}{5}$,
∴AB=2a=$\frac{4\sqrt{5}}{5}$.
(2)如图2中,连接EF.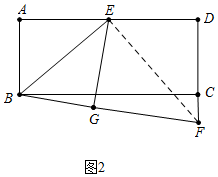
由(1)可知,△EFG≌△EFD,
∴∠FED=∠FEG,FD=FG,∵∠BEA=∠BEG,
∴∠BEF=90°,
∵∠BEG+∠FEG=90°,∠FEG+∠EFG=90°,
∠BEG=∠EFG,∵∠BGE=∠FGE=90°,
∴△BEG∽△EFG,
∴$\frac{EG}{FG}$=$\frac{BG}{EG}$,
∴EG2=BG•GF,设DC=AB=BG=a,则DF=FG=ka,
∴EG2=ka2,
∴EG=$\sqrt{k}$a,
∴AD=2EG=2$\sqrt{k}$a,
∴$\frac{AD}{AB}$=$\frac{2\sqrt{k}a}{a}$=2$\sqrt{k}$.
点评 本题考查翻折变换、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是正确性质全等三角形解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 对于平面直角坐标系中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
对于平面直角坐标系中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
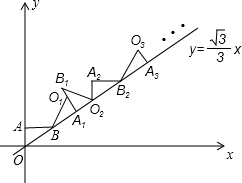 如图,A(0,1),B($\sqrt{3}$,1),将△ABO绕点B旋转到△A1B1O1的位置,点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1旋转到△A2B1O2的位置,点O1的对应点O2也落在直线上,依次下去…,若点则点B8坐标是(6+7$\sqrt{3}$,7+2$\sqrt{3}$).
如图,A(0,1),B($\sqrt{3}$,1),将△ABO绕点B旋转到△A1B1O1的位置,点A的对应点A1落在直线y=$\frac{\sqrt{3}}{3}$x上,再将△A1BO1绕点A1旋转到△A2B1O2的位置,点O1的对应点O2也落在直线上,依次下去…,若点则点B8坐标是(6+7$\sqrt{3}$,7+2$\sqrt{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(x>0)的图象与BC边交于点E.
如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=$\frac{k}{x}$(x>0)的图象与BC边交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
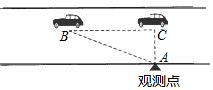 《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过75km/时.一辆“小汽车”在一条城市街道上直道行驶,如图某一时刻刚好行驶到路对面“车速检测仪A”正前方15m的C处,过了1秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为25m,这辆“小汽车”超速了吗?请说明理由.
《中华人民共和国道路交通管理条例》规定:小汽车在城市街道上的行驶速度不得超过75km/时.一辆“小汽车”在一条城市街道上直道行驶,如图某一时刻刚好行驶到路对面“车速检测仪A”正前方15m的C处,过了1秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为25m,这辆“小汽车”超速了吗?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com