
【题目】用适当的方法解下列方程:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() (4)
(4)![]() .
.
【答案】(1)x1=﹣![]() ,x2=
,x2=![]() ;(2)x1=3,x2=﹣3;(3)方程没有实数根;(4)x1=2,x2=
;(2)x1=3,x2=﹣3;(3)方程没有实数根;(4)x1=2,x2=![]() .
.
【解析】
(1)直接利用因式分解法求出解即可;
(2)先移项,再利用因式分解法求出解即可;
(3)先判断方程根的情况,可得到此方程没有实数根;
(4)利用公式法求出解即可.
解:(1)分解因式得,(2x+7)(2x﹣7)=0,
∴2x+7=0或2x﹣7=0,
∴x1=﹣![]() ,x2=
,x2=![]() ;
;
(2)移项,得(x﹣3)2﹣2x(x﹣3)=0,
∴(x﹣3)(x﹣3﹣2x)=0,
∴x﹣3=0或﹣x﹣3=0,
∴x1=3,x2=﹣3;
(3)∵a=1,b=1,c=3,
∴△=12﹣4×1×3=﹣11<0,
∴方程没有实数根;
(4)∵a=2,b=﹣1,c=﹣6,
∴△=(﹣1)2﹣4×2×(﹣6)=49>0,
∴![]() ,
,
∴x1=2,x2=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校九年级10个班级师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现唱歌类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟,若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型 | A型 | B型 |
进价(元/盏) | 40 | 65 |
售价(元/盏) | 60 | 100 |
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3![]() ,BC=7,求线段BD的长.
,BC=7,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聪聪、明明、伶伶、俐俐四人共同探究代数式![]() 的值的情况他们做了如下分工,聪聪负责找值为0时
的值的情况他们做了如下分工,聪聪负责找值为0时![]() 的值,明明负责找值为4时
的值,明明负责找值为4时![]() 的值,伶伶负责找最小值,俐俐负责找最大值,几分钟,各自通报探究的结论,其中正确的是( )
的值,伶伶负责找最小值,俐俐负责找最大值,几分钟,各自通报探究的结论,其中正确的是( )
(1)聪聪认为找不到实数![]() ,使
,使![]() 的值为0;
的值为0;
(2)明明认为只有当![]() 时,
时,![]() 的值为4;
的值为4;
(3)伶伶发现![]() 有最小值;(4)俐俐发现
有最小值;(4)俐俐发现![]() 有最大值
有最大值
A.(1)(2)B.(1)(3)C.(1)(4)D.(1)(2)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )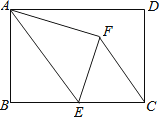
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,连接BE,EC.下列判断:①△ABE≌△DCE;②BE=EC;③BE⊥EC;④EC=![]() DE.其中正确的有( )
DE.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F.

(1)求证:GE=GF;
(2)填空:若BD=1,则DF的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个长方形的长和宽分别为x厘米和y厘米(x,y为正整数),如果将长方形的长和宽各增加5厘米得到新的长方形,面积记为![]() ,将长方形的长和宽各减少2厘米得到新的长方形,面积记为
,将长方形的长和宽各减少2厘米得到新的长方形,面积记为![]() .
.
(1)请说明:![]() 与
与![]() 的差一定是7的倍数.
的差一定是7的倍数.
(2)如果![]() 比
比![]() 大196
大196![]() ,求原长方形的周长.
,求原长方形的周长.
(3)如果一个面积为![]() 的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由.
的长方形和原长方形能够没有缝隙没有重叠的拼成一个新的长方形,请找出x与y的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com