
【题目】如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3![]() ,BC=7,求线段BD的长.
,BC=7,求线段BD的长.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】2017年5月14日至15日,“一带一路”国际合作高峰论坛在北京举行.本届论坛期间,中国同30多个国家签署经贸合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知2件甲种商品与3件乙种商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.
(1)甲种商品与乙种商品的销售单价各多少元?
(2)若甲、乙两种商品的销售总收入不低于5400万元,则至少销售甲种商品多少万件?
查看答案和解析>>
科目:初中数学 来源: 题型:
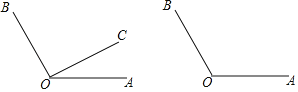
【题目】如图,∠AOB=120°,点C为平面内一点,作射线OC,射线OD平分∠BOC,射线OE平分∠AOD.
(1)若点C为∠AOB内部一点且∠AOC=30°,依题意补全图形,并求出∠EOC的度数;
(2)若点C为∠AOB内部一点,∠AOC=α(0<α<120°)直接用含α的代数式表示∠EOC的度数;
(3)若∠EOC=10°,请你直接写出所有符合条件的∠AOC度数(0<∠AOC<180°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.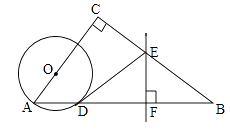
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形OABC移动一周(即:沿着O→A→B→C→O的路线移动)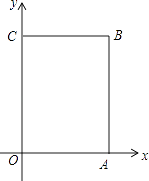
(1)写出B点的坐标();
(2)当点P移动了4秒时,在图中平面直角坐标系中描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴的距离为5个单位长度时,求点P移动的时间t.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )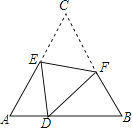
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com