
【题目】如图,D是等边△ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=( )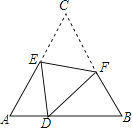
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:设AD=k,则DB=2k,
∵△ABC为等边三角形,
∴AB=AC=3k,∠A=∠B=∠C=∠EDF=60°,
∴∠EDA+∠FDB=120°,
又∵∠EDA+∠AED=120°,
∴∠FDB=∠AED,
∴△AED∽△BDF,
∴![]() ,
,
设CE=x,则ED=x,AE=3k﹣x,
设CF=y,则DF=y,FB=3k﹣y,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴CE:CF=4:5.
故选:B.
【考点精析】本题主要考查了翻折变换(折叠问题)和相似三角形的判定与性质的相关知识点,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A按顺时针方向旋转90°,得到△ADE,点B的对应点为点D,点C的对应点E落在BC边上,连接BD.
(1)求证:DE⊥BC;
(2)若AC=3![]() ,BC=7,求线段BD的长.
,BC=7,求线段BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则sin∠ECF=( )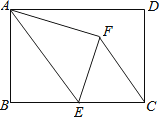
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板ADE如图放置,连接BE,EC.下列判断:①△ABE≌△DCE;②BE=EC;③BE⊥EC;④EC=![]() DE.其中正确的有( )
DE.其中正确的有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB交AB于点E,且CD=AC,DF∥BC,分别与AB,AC交于点G,F.

(1)求证:GE=GF;
(2)填空:若BD=1,则DF的长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施居民用水阶梯价格制度,按年度用水量计算,将居民家庭全年用水量划分为三个阶梯,水价按阶梯递增:
第一阶梯:年用水量不超过200吨,每吨水价为3元;
第二阶梯:年用水量超过200吨但不超过300吨的部分,每吨水价为3. 5元;
第三阶梯:年用水量超过300吨的部分,每吨水价为6元.
(1)小明家2018年用水180吨,这一年应缴纳水费 元;
(2)小亮家2018年缴纳水费810元,则小亮家这一年用水多少吨?
(3)小红家2017年和2018年共用水600吨,共缴纳水费1950元,并且2018年的用水量超过2017年的用水量,则小红家2017年和2018年各用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 和点
和点![]() 关于原点对称,点
关于原点对称,点![]() 是直线
是直线![]() 位于
位于![]() 轴右侧部分图象上一点,连接
轴右侧部分图象上一点,连接![]() ,已知
,已知![]() .
.
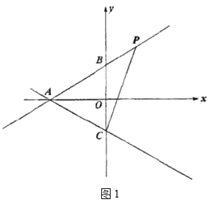
(1)求直线![]() 的解析式;
的解析式;
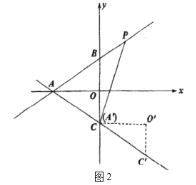
(2)如图2,![]() 沿着直线
沿着直线![]() 平移得
平移得![]() ,平移后的点
,平移后的点![]() 与点
与点![]() 重合.点
重合.点![]() 为直线
为直线![]() 上的一动点,当
上的一动点,当![]() 的值最小时,请求出
的值最小时,请求出![]() 的最小值及此时点
的最小值及此时点![]() 的坐标;
的坐标;
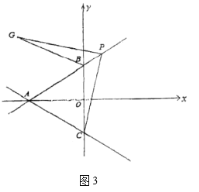
(3)如图3,将![]() 沿直线
沿直线![]() 是翻折得
是翻折得![]() 点
点![]() 为平面内任意一动点,在直线
为平面内任意一动点,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得以点
,使得以点![]() 为顶点的四边形是矩形;若存在,请直接写出点
为顶点的四边形是矩形;若存在,请直接写出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com