
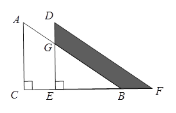
【题目】如图所示,将直角三角形ACB, ![]() ,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=
,AC=6,沿CB方向平移得直角三角形DEF,BF=2,DG=![]() ,阴影部分面积为_______.
,阴影部分面积为_______.
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,AF∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.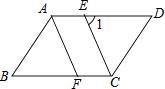
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学的1号教学大楼共有4道门,其中两道正门大小相同,两道侧门也大小相同,安全检查时,对4道门进行了测试,当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生,当同时开启一道正门和一道侧门时,4分钟内可通过800名学生.
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)该中学的2号教学大楼,有和1号教学大楼相同的正门和侧门共5道,若这栋大楼的教室里最多有1920名学生,安全检查规定,在紧急情况下,全大楼学生应在4分钟内通过这5道门安全撤离,该栋大楼正门和侧门各有几道?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一张两边分别平行的纸条折成如图所示,EF为折痕,ED交BF于点G,且∠EFB=48°,则下列结论: ①∠DEF=48°;②∠AED=84°;③∠BFC=84°;④∠DGF=96°,其中正确的个数有( )
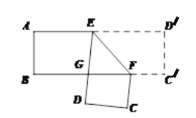
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
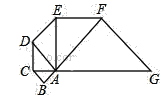
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
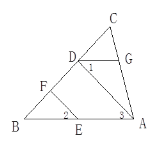
解: 因为EF∥AD,
所以∠2=____ (_________________________________)
又因为∠1=∠2
所以∠1=∠3 (__________________)
所以AB∥_____ (___________________________________)
所以∠BAC+______=180°(___________________________)
因为∠BAC=70°
所以∠AGD=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,AB∥EG∥x轴,BC∥DE∥HG∥AP∥y轴,点D、C、P、H在x轴上,A(1,2),B(﹣1,2),D(﹣3,0),E(﹣3,﹣2),G(3,﹣2),把一条长为2018个单位长度且没有弹性的细线线的粗细忽略不计)的一端固定在点A处,并按A﹣B﹣C﹣D﹣E﹣F﹣G﹣H﹣﹣P﹣A…的规律紧绕在图形“凸”的边上,则细线另一端所在位置的点的坐标是( )
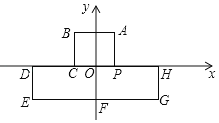
A. (1,2)B. (﹣1,2)C. (﹣1,0)D. (1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生的特长爱好,提髙学生的综合素质,某校音乐特色学习班准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买2个竖笛和1个尤克里里共需290元;竖笛单价比尤克里里单价的一半少25元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共20个,但要求购买竖笛和尤克里里的总费用不超过3450元,则该校最多可以购买多少个尤克里里?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com