
【题目】某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收人=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?
【答案】
(1)解:当40≤x≤58时,设y与x的函数解析式为y=k1x+b1,由图象可得
![]() ,
,
解得 ![]() .
.
∴y=﹣2x+140.
当58<x≤71时,设y与x的函数解析式为y=k2x+b2,由图象得
![]() ,
,
解得 ![]() ,
,
∴y=﹣x+82,
综上所述:y= ![]() ;
;
(2)解:设人数为a,当x=48时,y=﹣2×48+140=44,
∴(48﹣40)×44=106+82a,
解得a=3;
(3)解:设需要b天,该店还清所有债务,则:
b[(x﹣40)y﹣82×2﹣106]≥68400,
∴b≥ ![]() ,
,
当40≤x≤58时,∴b≥ ![]() =
= ![]() ,
,
x=﹣ ![]() 时,﹣2x2+220x﹣5870的最大值为180,
时,﹣2x2+220x﹣5870的最大值为180,
∴b ![]() ,即b≥380;
,即b≥380;
当58<x≤71时,b ![]() =
= ![]() ,
,
当x=﹣ ![]() =61时,﹣x2+122x﹣3550的最大值为171,
=61时,﹣x2+122x﹣3550的最大值为171,
∴b ![]() ,即b≥400.
,即b≥400.
综合两种情形得b≥380,即该店最早需要380天能还清所有债务,此时每件服装的价格应定为55元.
【解析】(1)根据待定系数法,可得函数解析式;(2)根据收入等于指出,可得一元一次方程,根据解一元一次方程,可得答案;(3)分类讨论40≤x≤58,或58≤x≤71,根据收入减去支出大于或等于债务,可得不等式,根据解不等式,可得答案.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,BD、CE是高,BD与CE相交于点O 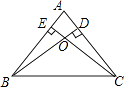
(1)求证:OB=OC;
(2)若∠ABC=50°,求∠BOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点M为抛物线y=﹣x2+2nx﹣n2+2n的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线y=﹣x2+2nx﹣n2+2n绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), ![]() .
.
写出C点的坐标:C( , )(坐标用含有t的代数式表示);
(4)若点C在题(2)中旋转后的新抛物线上,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2 , 则成绩较为整齐的是队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为x小时,两车之间的距离为y千米,图中折线表示y与x之间的函数图象,请根据图象解决下列问题: 
(1)甲乙两地之间的距离为千米;
(2)求快车和慢车的速度;
(3)求线段DE所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为 ![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.连续抛一均匀硬币2次必有1次正面朝上
B.连续抛一均匀硬币10次都可能正面朝上
C.大量反复抛一均匀硬币,平均100次出现正面朝上50次
D.通过抛一均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com