
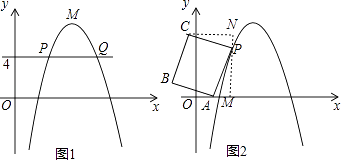
【题目】如图1,在平面直角坐标系xOy中,点M为抛物线y=﹣x2+2nx﹣n2+2n的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线y=﹣x2+2nx﹣n2+2n绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), ![]() .
.
写出C点的坐标:C( , )(坐标用含有t的代数式表示);
(4)若点C在题(2)中旋转后的新抛物线上,求t的值.
【答案】
(1)
解:∵抛物线y=﹣x2+2nx﹣n2+2n过点P,P点的纵坐标为4,
∴4=﹣x2+2nx﹣n2+2n
解得:x1=n+ ![]() ,x2=n﹣
,x2=n﹣ ![]() ,
,
∵PQ=x1﹣x2=4,
∴2 ![]() =4,
=4,
解得:n=4,
∴抛物线的函数关系式为:y=﹣x2+8x﹣8,
∴4=﹣x2+8x﹣8,
解得:x=2或x=6,
∴P(2,4).
(2)
解:正确;
∵P(2,4),PQ=4,
∴Q绕着点P旋转180°后的对称点为Q′(﹣2,4),
∴P与Q′正好关于y轴对称,
∴所得新抛物线的对称轴是y轴,
∵抛物线y=﹣x2+8x﹣8=﹣(x﹣4)2+8,
∴抛物线的顶点M(4,8),
∴顶点M到直线PQ的距离为4,
∴所得新抛物线顶点到直线PQ的距离为4,
∴所得新抛物线顶点应为坐标原点.
(3)﹣4t+2;4+t
(4)
解:由(1)可知,旋转后的新抛物线是y=ax2,
∵新抛物线是y=ax2过P(2,4),
∴4=4a,
∴a=1,
∴旋转后的新抛物线是y=x2,
∵C(﹣4t+2,4+t)在抛物线y=x2上,
∴4+t=(﹣4t+2)2,
解得:t=0(舍去)或t= ![]() ,
,
∴t= ![]() .
.
【解析】解:(3)如图2,过P作x轴的垂线,交x轴于M,过C作CN⊥MN于N,
∵ ![]() ,
,
∴ ![]() =
= ![]() ,
,
∵△APM∽△PCN,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∵AM=2﹣1=1,PM=4,
∴PN=t,CN=4t,
∴MN=4+t,
∴C(﹣4t+2,4+t),
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AM为⊙O的切线,A为切点,过⊙O上一点B作BD⊥AM于点D,BD交⊙O于点C,OC平分∠AOB. 
(1)求∠AOB的度数;
(2)当⊙O的半径为2cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点P在射线BC上(异于点B、C),直线AP与对角线BD及射线DC分别交于点F、Q 
(1)若BP= ![]() ,求∠BAP的度数;
,求∠BAP的度数;
(2)若点P在线段BC上,过点F作FG⊥CD,垂足为G,当△FGC≌△QCP时,求PC的长;
(3)以PQ为直径作⊙M. ①判断FC和⊙M的位置关系,并说明理由;
②当直线BD与⊙M相切时,直接写出PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一只不透明的布袋中装有红球、黄球各若干个,这些球除颜色外都相同,充分摇匀.
(1)若布袋中有3个红球,1个黄球.从布袋中一次摸出2个球,计算“摸出的球恰是一红一黄”的概率(用“画树状图”或“列表”的方法写出计算过程);
(2)若布袋中有3个红球,x个黄球. 请写出一个x的值 , 使得事件“从布袋中一次摸出4个球,都是黄球”是不可能的事件;
(3)若布袋中有3个红球,4个黄球. 我们知道:“从袋中一次摸出4个球,至少有一个黄球”为必然事件.
请你仿照这个表述,设计一个必然事件: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a1 , a2 , …,a2014是从1,0,﹣1这三个数中取值的一列数,若a1+a2+…+a2014=69,(a1+1)2+(a2+1)2+…+(a2014+1)2=4001,则a1 , a2 , …,a2014中为0的个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店因为经营不善欠下38400元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息).已知该店代理的品牌服装的进价为每件40元,该品牌服装日销售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含债务). 
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)若该店暂不考虑偿还债务,当某天的销售价为48元/件时,当天正好收支平衡(收人=支出),求该店员工的人数;
(3)若该店只有2名员工,则该店最早需要多少天能还清所有债务,此时每件服装的价格应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com