Question

7．如图，某广场为矩形ABCD，现准备在广场的内部修建照明灯，要求照明灯0到广场的两个人口A，D的距离相等，且到AB，BC两边的距离相等．
（1）用直尺和圆规作出点0的位置．（不写作法，保留作图痕迹）
（2）已知AB=320m，AD=400m，求0B的距离．

Answer 1

分析 （1）到A，D的距离相等的点在AD的垂直平分线上，到AB，BC两边的距离相等的点在∠ABC的平分线上；
（2）由（1）可知△OBE为等腰直角三角形，由勾股定理可求得OB的长．

解答 解：（1）如图1所示：

（2）如图2所示：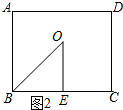

∵由（1）可知OE垂直平分BC，BO平分∠ABC，
∴∠OEB=90°，OE=BE=$\frac{1}{2}AD$=200m．
在Rt△OBE中，由勾股定理得：OB=$\sqrt{E{B}^{2}+O{E}^{2}}$=200$\sqrt{2}$．
∴OB=200$\sqrt{2}$m．

点评 本题主要考查作图-应用与设计，依据线段垂直平分线的性质和角平分线的性质确定出点O的位置是解题的关键．