
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连结PM并延长到点E,使ME=PM,连结DE.
(1)请你利用图2,选择Rt△ABC内的任意一点P按上述方法操作;

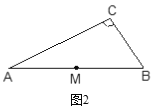
(2)经历(1)之后,观察两图形,猜想线段DE和线段BC之间有怎样的数量和位置关系?请选择其中的一个图形证明你的猜想;
(3)观察两图,你还可得出AC和DE相关的什么结论?请说明理由.
(4)若以A为坐标原点,建立平面直角坐标系,其中A、C、D的坐标分别为(0,0),(5,3),(4,2),能否在平面内找到一点M,使以A、C、D、M为点构造成平行四边形,若不能,说明理由,若能,请直接写出点M的坐标.
【答案】(1)见解析;(2)DE//BC;DE=BC;(3)DE⊥AC;(4)M(1,1)或(-1,-1)或(9,5).
【解析】
(1)根据图1的构图条件,在Rt△ABC内的任取一点P,作图即可;
(2)连接BE,根据边角边可证△PAM和△EBM全等,可得EB和PA既平行又相等,而PA和CD既平行且相等,所以DE和BC平行相等,
(3)由(2)得BC⊥AC,DE∥BC,所以DE也和AC垂直;
(4)以A、C、D、M为点构造成平行四边形的顶点顺序没定,故有三种情况:分别过点A,C,D作线段CD,AD,AC的平行线,三条直线的交点即为能以A、C、D、M为点构造成平行四边形的点M的位置,再利用平行四边形的性质及平移知识即可求得点M 的坐标
解:(1)作图如图2:
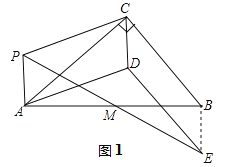
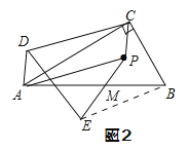
(2)观察图1,图2,猜想线段DE和线段BC数量和位置关系为:DE=BC,DE//BC;
选择图1,证明如下:
连接BE,
∵PM=ME,∠PMA=∠EMB,AM=MB,
∴△PMA≌△EMB.(SAS)
∵PA=BE,∠MPA=∠MEB,
∴PA∥BE.
∵平行四边形PADC,
∴PA∥DC,PA=DC.
∴BE∥DC,BE=DC,
∴四边形DEBC是平行四边形.
∴DE∥BC,DE=BC.
(3)猜想DE⊥AC;理由如下:
∵∠ACB=90°,
∴BC⊥AC,
又∵DE∥BC,(已证)
∴DE⊥AC.
(3)如图3
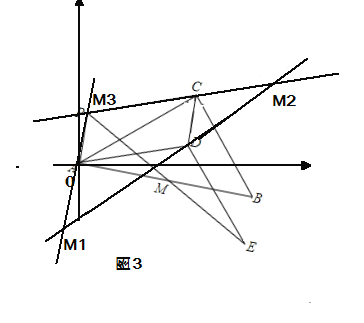
分别过点A,C,D作线段CD,AD,AC的平行线,三条直线分别相交于点![]() ,则得到
,则得到![]() 即为满足条件的点M,使以A、C、D、M为点构造成平行四边形.理由如下:
即为满足条件的点M,使以A、C、D、M为点构造成平行四边形.理由如下:
∵AC//DM1,CD//AM1,
∴四边形ACDM1为平行四边形,
同理可得:四边形ACM2D为平行四边形,四边形ADCM3为平行四边形.
设M1的坐标为(x,y),
由于四边形ACDM1为平行四边形,
∴AC//M1D,AC=M1D.可以看做线段AC经过适当的平移到线段M1D.
C与D为对应点,A与M1为对应点,
易知:点C(5,3)向左平移一个单位,向下平移一个单位得到D(4,2).
故点A也向左平移一个单位,向下平移一个单位得到M1(x,y),即
0-1=x,0-1=y,所以x=-1,y=-1.点M1的坐标为(-1,-1),同理可得
M2的坐标为(9,5),M3的坐标为(1,1).
故存在M点,分别为(1,1)或(-1,-1)或(9,5).使以A、C、D、M为点构造成平行四边形


科目:初中数学 来源: 题型:
【题目】甲、乙两工程队承包一项工程,如果甲工程队单独施工,恰好如期完成;如果乙工程队单独施工就要超过6个月才能完成,现在甲、乙两队先共同施工4个月,剩下的由乙队单独施工,则恰好如期完成.
(1)问原来规定修好这条公路需多少长时间?
(2)现要求甲、乙两个工程队都参加这项工程,但由于受到施工场地条件限制,甲、乙两工程队不能同时施工.已知甲工程队每月的施工费用为4万元,乙工程队每月的施工费用为2万元.为了结算方便,要求:甲、乙的施工时间为整数个月,不超过15个月完成.当施工费用最低时,甲、乙各施工了多少个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣ ![]() ≤x<n+
≤x<n+ ![]() ,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
,则[x]=n.如:[3.4]=3,[3.5]=4,…根据以上材料,解决下列问题:
(1)填空:
①若[x]=3,则x应满足的条件:________;
②若[3x+1]=3,则x应满足的条件:________;
(2)求满足[x]= ![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市举行店庆活动,对甲、乙两种商品实行打折销售,打折前,购买2件甲商品和3件乙商品需要180元;购买1件甲商品和4件乙商品需要200元,而店庆期间,购买10件甲商品和10件乙商品仅需520元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点O是边AC上一个动点,过点O作直线
中,点O是边AC上一个动点,过点O作直线![]() //BC,分别交
//BC,分别交![]() ,外角
,外角![]() 的平分线于点E、F.
的平分线于点E、F.

(1)猜想与证明,试猜想线段OE与OF的数量关系,并说明理由.
(2)连接AE,AF,问:当点O在边AC上运动时到什么位置时,四边形AECF是矩形?并说明理由.
(3)若AC边上存在一点O,使四边形AECF是正方形,猜想![]() 的形状并证明你的结论.
的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移6个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度) .

(1)在图中画出平移后的△A1B1C1;
(2)直接写出△A1B1C1各顶点的坐标.
![]() ;
; ![]() ;
; ![]() ;
;
(3)求出△ABC的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
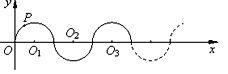
【题目】如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2019秒时,点P的坐标是________________
个单位长度,则第2019秒时,点P的坐标是________________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com