
【题目】(1)如图1,直线AB∥CD,点P在两平行线之间,写出∠BAP、∠APC、∠DCP满足的数量关系.
(2)如图2,直线AB与CD相交于点E,点P为∠AEC内一点,AQ平分∠EAP,CQ平分∠ECP,若∠AEC=40°,∠AQC=70°,求∠APC的度数.
(3)如图3,连接AD、CB交于点P,AQ平分∠BAD,CQ平分∠BCD,探究∠ABC、∠AQC、∠ADC满足的关系.

【答案】(1)∠BAP+∠DCP=∠APC;(2)100°;(3)∠ABC+∠ADC=2∠AQC.
【解析】
(1)过P作PE∥AB,利用平行线的性质:两直线平行内错角相等,易得到∠BAP、∠APC、∠DCP间关系;
(2)连接EQ并延长至G,连接QP并延长到H,利用角平分线的性质和三角形的外角等于不相邻的两个内角的关系,先得到∠QAP+∠QCP=30°,再得到∠APC的度数.
(3)利用角平分线的性质,得到∠BAQ=∠QAD,∠DCQ=∠QCB,利用三角形的外角等于不相邻的两个内角,通过∠BEQ、∠DFQ把∠ABC、∠AQC、∠ADC、连接起来得到结论.
解:(1)如图1所示,过P作PE∥AB,
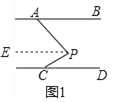
∵AB∥CD,∴PE∥CD
∵PE∥AB,∴∠BAP=∠APE,
同理,∠DCP=∠CPE
∴∠BAP+∠DCP=∠APE+∠CPE=∠APC
故答案为:∠BAP+∠DCP=∠APC,
(2)连接EQ并延长至G,
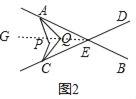
∵AQ平分∠EAP,CQ平分∠ECP,
∴∠EAQ=∠QAP,∠ECQ=∠QCP
∵∠AQG=∠QAE+∠AEQ,∠CQG=∠QCE+∠CEQ,
∴∠AQG+∠CQG=∠QAE+∠AEQ+∠QCE+∠CEQ,
即∠AQC=∠CEA+∠QAE+∠QCE
∵∠AEC=40°,∠AQC=70°
∴∠QAE+∠QCE=30°
即∠QAP+∠QCP=30°
连接QP并延长到H.
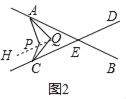
∵∠APH=∠AQP+∠PAQ,∠CPH=∠PQC+∠PCQ,
∴∠APH+∠CPH=∠AQP+∠PAQ+∠PQC+∠PCQ,
即∠APC=∠CQA+∠QAP+∠QCP
∴∠APC=30°+70°=100°.
(3)如图3中,
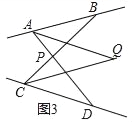
∵AQ平分∠BAD,CQ平分∠BCD,
∴∠BAQ=∠QAD,∠DCQ=∠QCB
∵∠BEQ=∠ABC+∠BAQ=∠BCQ+∠AQC,
∵∠QFD=∠ADC+∠QCD=∠QAD+∠AQC,
∴∠ABC+∠BAQ+∠ADC+∠QCD=∠BCQ+∠AQC+∠QAD+∠AQC
即∠ABC+∠ADC=2∠AQC.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】我州某养殖场计划购买甲、乙两种鱼苗600条,甲种鱼苗每条16元,乙种鱼苗每条20元,相关资料表明:甲、乙两种鱼苗的成活率为80%,90%
(1)若购买这两种鱼苗共用去11000元,则甲、乙两种鱼苗各购买多少条?
(2)若要使这批鱼苗的总成活率不低于85%,则乙种鱼苗至少购买多少条?
(3)在(2)的条件下,应如何选购鱼苗,使购买鱼苗的总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( )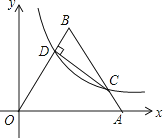
A.25 ![]()
B.18 ![]()
C.9 ![]()
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是边长为4cm的正方形ABCD的中心,M是BC的中点,动点P由A开始沿折线A﹣B﹣M方向匀速运动,到M时停止运动,速度为1cm/s.设P点的运动时间为t(s),点P的运动路径与OA、OP所围成的图形面积为S(cm2),则描述面积S(cm2)与时间t(s)的关系的图象可以是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是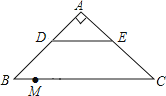
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒 ![]() cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解学生的体能情况,随机选取了1000名学生进行调查,并记录了他们对长跑、短跑、跳绳、跳远四个项目的喜欢情况,整理成以下统计表,其中“√”表示喜欢,“×”表示不喜欢.
项目 | 长跑 | 短跑 | 跳绳 | 跳远 |
200 | √ | × | √ | √ |
300 | × | √ | × | √ |
150 | √ | √ | √ | × |
200 | √ | × | √ | × |
150 | √ | × | × | × |
(1)估计学生同时喜欢短跑和跳绳的概率;
(2)估计学生在长跑、短跑、跳绳、跳远中同时喜欢三个项目的概率;
(3)如果学生喜欢长跑、则该同学同时喜欢短跑、跳绳、跳远中哪项的可能性大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.
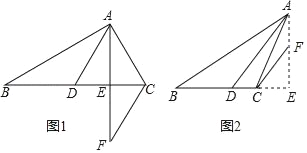
(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;
(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)
(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com