Question

【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时，发现了“中垂三角形”，即两条中线互相垂直的三角形称为“中垂三角形”．如图（1）、图（2）、图（3）中，AM、BN是△ABC的中线，AN⊥BN于点P，像△ABC这样的三角形均为“中垂三角形”．设BC=a，AC=b，AB=c．
【特例探究】

（1）如图1，当tan∠PAB=1，c=4 时，a= ， b=；
如图2，当∠PAB=30°，c=2时，a= ， b=；
（2）【归纳证明】请你观察（1）中的计算结果，猜想a2、b2、c2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
（3）【拓展证明】如图4，ABCD中，E、F分别是AD、BC的三等分点，且AD=3AE，BC=3BF，连接AF、BE、CE，且BE⊥CE于E，AF与BE相交点G，AD=3 ，AB=3，求AF的长．

Answer 1

【答案】
（1）4 ；4 ；；
（2）

结论a2+b2=5c2．

证明：如图3中，

连接EF．

∵AF、BE是中线，

∴EF∥AB，EF= AB，

∴△FPE∽△APB，

∴ = = ，

设FP=x，EP=y，则AP=2x，BP=2y，

∴a2=BC2=4BF2=4（FP2+BP2）=4x2+16y2，

b2=AC2=4AE2=4（PE2+AP2）=4y2+16x2，

c2=AB2=AP2+BP2=4x2+4y2，

∴a2+b2=20x2+20y2=5（4x2+4y2）=5c2．

（3）

解：如图4中，

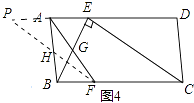
在△AGE和△FGB中，

，

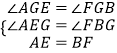∴△AGE≌△FGB，

∴BG=FG，取AB中点H，连接FH并且延长交DA的延长线于P点，

同理可证△APH≌△BFH，

∴AP=BF，PE=CF=2BF，

即PE∥CF，PE=CF，

∴四边形CEPF是平行四边形，

∴FP∥CE，

∵BE⊥CE，

∴FP⊥BE，即FH⊥BG，

∴△ABF是中垂三角形，

由（2）可知AB2+AF2=5BF2，

∵AB=3，BF= AD= ，

∴9+AF2=5×（ ）2，

∴AF=4．

【解析】（1）解：如图1中，

∵CE=AE，CF=BF，
∴EF∥AB，EF= AB=2 ，
∵tan∠PAB=1，
∴∠PAB=∠PBA=∠PEF=∠PFE=45°，
∴PF=PE=2，PB=PA=4，
∴AE=BF= =2 ．
∴b=AC=2AE=4 ，a=BC=4 ．
故答案为4 ，4 ．
如图2中，

连接EF，
， ∵CE=AE，CF=BF，
∴EF∥AB，EF= AB=1，
∵∠PAB=30°，
∴PB=1，PA= ，
在RT△EFP中，∵∠EFP=∠PAB=30°，
∴PE= ，PF= ，
∴AE= = ，BF= = ，
∴a=BC=2BF= ，b=AC=2AE= ，
故答案分别为 ， ．
（1）①首先证明△APB，△PEF都是等腰直角三角形，求出PA、PB、PE、PF，再利用勾股定理即可解决问题．
②连接EF，在RT△PAB，RT△PEF中，利用30°性质求出PA、PB、PE、PF，再利用勾股定理即可解决问题．（2）结论a2+b2=5c2 ． 设MP=x，NP=y，则AP=2x，BP=2y，利用勾股定理分别求出a2、b2、c2即可解决问题．（3）取AB中点H，连接FH并且延长交DA的延长线于P点，首先证明△ABF是中垂三角形，利用（2）中结论列出方程即可解决问题．本题考查四边形综合题、三角形中位线定理、平行四边形的判定和性质、勾股定理等知识，解题的关键是理解题意，学会添加常用辅助线构造全等三角形，学会利用新的结论解决问题，属于中考压轴题．