Question

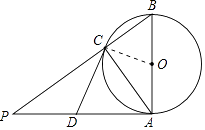
【题目】如图，AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C，点D为AP的中点，连结AC．求证：
（1）∠P=∠BAC
（2）直线CD是⊙O的切线．

Answer 1

【答案】
（1）解：证明：∵AB是⊙O的直径，

∴∠ACB=90°，

∴∠ACP=90°，

∴∠P+∠CAP=90°，

∵AP⊙O是切线，

∴∠BAP=90°，

即∠CAP+∠BAC=90°

∴∠P=∠BAC；

（2）解：∵CD是Rt△PAC斜边PA的中线，

∴CD=AD，

∴∠DCA=∠DAC，

连接OC，

∵OC=OA，

∴∠OCA=∠OAC，

∴∠DCO=∠DAO=90°，

∴CD是⊙O的切线．

【解析】（1）要证明∠P=∠BAC，只要证明∠CAP+∠BAC=∠P+∠CAP即可，根据题目中的条件可以证明它们相等，从而可以解答本题；（2）要证明直线CD是⊙O的切线，只要证明∠OCD=90°即可，根据题目中的条件和（1）中的结论可以证明∠OCD=90°，从而可以解答本题．