Question

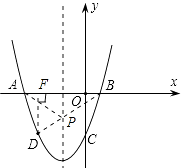
【题目】已知二次函数y=x2+bx+c的图象过点A（﹣3，0）和点B（1，0），且与y轴交于点C，D点在抛物线上且横坐标是﹣2．

（1）求抛物线的解析式；
（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值．

Answer 1

【答案】
（1）

解：将A（﹣3，0），B（1，0）代入y=x2+bx+c，

得 ，

解得

∴y=x2+2x﹣3

（2）

解：∵y=x2+2x﹣3=（x+1）2﹣4

∴对称轴x=﹣1，

又∵A，B关于对称轴对称，

∴连接BD与对称轴的交点即为所求P点．

过D作DF⊥x轴于F．将x=﹣2代入y=x2+2x﹣3，

则y=4﹣4﹣3=﹣3，

∴D（﹣2，﹣3）

∴DF=3，BF=1﹣（﹣2）=3

Rt△BDF中，BD=

∵PA=PB，

∴PA+PD=BD= ．

故PA+PD的最小值为 ．

【解析】（1）把A（﹣3，0）和点B（1，0），代入y=x2+bx+c，建立关于b，c的二元一次方程组，求出b，c即可；（2）先求出抛物线的对称轴，又因为A，B关于对称轴对称，所以连接BD与对称轴的交点即为所求P点．
【考点精析】根据题目的已知条件，利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．