
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЪЧзјБъдЕуЃЌГЄЗНаЮOACBЕФЖЅЕуAЁЂBЗжБ№дкxжсгыyжсЩЯЃЌвбжЊOA=6ЃЌOB=10ЃЎЕуDЮЊyжсЩЯвЛЕуЃЌЦфзјБъЮЊ(0ЃЌ2)ЃЌЕуPДгЕуAГіЗЂвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЯпЖЮACЉCBЕФЗНЯђдЫЖЏЃЌЕБЕуPгыЕуBжиКЯЪБЭЃжЙдЫЖЏЃЌдЫЖЏЪБМфЮЊtУыЃЎ
(1)ЕБЕуPОЙ§ЕуCЪБЃЌЧѓжБЯпDPЕФКЏЪ§НтЮіЪНЃЛ
(2)ШчЭМЂкЃЌАбГЄЗНаЮбизХOPелЕўЃЌЕуBЕФЖдгІЕуBЁфЧЁКУТфдкACБпЩЯЃЌЧѓЕуPЕФзјБъЃЎ
(3)ЕуPдкдЫЖЏЙ§ГЬжаЪЧЗёДцдкЪЙЁїBDPЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1) y=![]() x+2ЃЛ(2)МћНтЮіЃЛ(3)ДцдкЃЌТњзуЬтвтЕФPзјБъЮЊ(6ЃЌ 6)Лђ(6ЃЌ
x+2ЃЛ(2)МћНтЮіЃЛ(3)ДцдкЃЌТњзуЬтвтЕФPзјБъЮЊ(6ЃЌ 6)Лђ(6ЃЌ ![]() )Лђ(6ЃЌ
)Лђ(6ЃЌ![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшжБЯпDPНтЮіЪНЮЊy=kx+bЃЌНЋDгыBзјБъДњШыЧѓГіkгыbЕФжЕЃЌМДПЩШЗЖЈГіНтЮіЪНЃЛЃЈ2ЃЉЂйЕБPдкACЖЮЪБЃЌШ§НЧаЮODPЕзODгыИпЮЊЙЬЖЈжЕЃЌЧѓГіДЫЪБУцЛ§ЃЛЕБPдкBCЖЮЪБЃЌЕзБпODЮЊЙЬЖЈжЕЃЌБэЪОГіИпЃЌМДПЩСаГіSгыtЕФЙиЯЕЪНЃЛЂкЕБЕуBЕФЖдгІЕуBЁфЧЁКУТфдкACБпЩЯЪБЃЌЙиМќЙДЙЩЖЈРэМДПЩЧѓГіДЫЪБPзјБъЃЛЃЈ3ЃЉДцдкЃЌЗжБ№вдBDЃЌDPЃЌBPЮЊЕзБпШ§жжЧщПіПМТЧЃЌРћгУЙДЙЩЖЈРэМАЭМаЮгызјБъаджЪЧѓГіPзјБъМДПЩЃЎ
(1)ЁпOA=6ЃЌOB=10ЃЌЫФБпаЮ OACB ЮЊГЄЗНаЮЃЌЁрC(6ЃЌ10)ЃЎ ЩшДЫЪБжБЯп DP НтЮіЪНЮЊ y=kx+bЃЌ
Аб(0ЃЌ2)ЃЌC(6ЃЌ10)ЗжБ№ДњШыЃЌЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ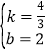 ЃЌ
ЃЌ
дђДЫЪБжБЯп DP НтЮіЪНЮЊ y=![]() x+2ЃЛ
x+2ЃЛ

(2)ЂйЕБЕу P дкЯпЖЮ AC ЩЯЪБЃЌOD=2ЃЌИпЮЊ 6ЃЌS=6ЃЛ ЕБЕу P дкЯпЖЮ BC ЩЯЪБЃЌOD=2ЃЌИпЮЊ 6+10Ѓ2t=16Ѓ2tЃЌS= 1 ЁС2ЁС(16Ѓ2t)=Ѓ2t+16ЃЛ
ЂкЩш P(m,10ЃЉЃЌдђPB=![]() =mЃЌШчЭМ 2ЃЌ Ёп
=mЃЌШчЭМ 2ЃЌ Ёп![]() =OB=10ЃЌ OA=6ЃЌ
=OB=10ЃЌ OA=6ЃЌ

Ёр![]() Ёр
Ёр![]() =10Ѓ8=2ЃЌ
=10Ѓ8=2ЃЌ
ЁпPC=6ЃmЃЌЁрm2=22+(6Ѓm)2ЃЌНтЕУm=![]() ЃЌдђДЫЪБЕуPЕФзјБъЪЧ(
ЃЌдђДЫЪБЕуPЕФзјБъЪЧ(![]() ЃЌ10)ЃЛ
ЃЌ10)ЃЛ
(3)ДцдкЃЌРэгЩЮЊЃКШєЁїBDPЮЊЕШбќШ§НЧаЮЃЌЗжШ§жжЧщПіПМТЧЃКШчЭМ3ЃЌ
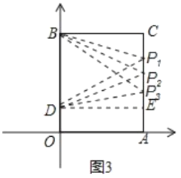
ЂйBD=BPl=OBЃOD=10Ѓ2=8ЃЌдк RtЁїBCP1 жаЃЌBP1=8ЃЌ BC=6ЃЌ
ИљОнЙДЙЩЖЈРэЕУЃК![]() ЃЌМДP1(6ЃЌ
ЃЌМДP1(6ЃЌ![]() )ЃЛ
)ЃЛ
ЂкЕБBP2= DP2ЪБЃЌДЫЪБP2(6ЃЌ6)ЃЛ
ЂлЕБDB=DP3=8ЪБЃЌдкRtЁїDEP3жаЃЌDE=6ЃЌИљОнЙДЙЩЖЈРэЕУЃК
![]() ЃЌЁр
ЃЌЁр![]() ЃЌМДP3 (6ЃЌ
ЃЌМДP3 (6ЃЌ![]() )ЃЌ
)ЃЌ
злЩЯЃЌТњзуЬтвтЕФPзјБъЮЊ(6ЃЌ 6)Лђ(6ЃЌ ![]() )Лђ(6ЃЌ
)Лђ(6ЃЌ![]() )ЃЎ
)ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаУќЬтЃЌецУќЬтЪЧЃЈ ЃЉ 
A.ШчЭМЃЌШчЙћOPЦНЗжЁЯAOBЃЌФЧУДЃЌPA=PB
B.Ш§НЧаЮЕФвЛИіЭтНЧДѓгкЫќЕФвЛИіФкНЧ
C.ШчЙћСНЬѕжБЯпУЛгаЙЋЙВЕуЃЌФЧУДетСНЬѕжБЯпЛЅЯрЦНаа
D.гавЛзщСкБпЯрЕШЕФОиаЮЪЧе§ЗНаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌАбЕуPЃЈЉ5ЃЌ3ЃЉЯђгвЦНвЦ8ИіЕЅЮЛЕУЕНЕуP1 ЃЌ дйНЋЕуP1ШЦдЕуа§зЊ90ЁуЕУЕНЕуP2 ЃЌ дђЕуP2ЕФзјБъЪЧЃЈ ЃЉ
A.ЃЈ3ЃЌЉ3ЃЉ
B.ЃЈЉ3ЃЌ3ЃЉ
C.ЃЈ3ЃЌ3ЃЉЛђЃЈЉ3ЃЌЉ3ЃЉ
D.ЃЈ3ЃЌЉ3ЃЉЛђЃЈЉ3ЃЌ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРквЊжЦзївЛИіШ§НЧаЮЕФИжМмФЃаЭЃЌдкетИіШ§НЧаЮжаЃЌГЄЖШЮЊxЃЈЕЅЮЛЃКcmЃЉЕФБпгыетЬѕБпЩЯЕФИпжЎКЭЮЊ40cmЃЌетИіШ§НЧаЮЕФУцЛ§SЃЈЕЅЮЛЃКcm2ЃЉЫцxЃЈЕЅЮЛЃКcmЃЉЕФБфЛЏЖјБфЛЏЃЎ
ЃЈ1ЃЉЧыжБНгаДГіSгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЈВЛвЊЧѓаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉЕБxЪЧЖрЩйЪБЃЌетИіШ§НЧаЮУцЛ§SзюДѓЃПзюДѓУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППЮЬУЩЯбЇЯАСЫЙДЙЩЖЈРэКѓЃЌжЊЕРЁАЙДШ§ЁЂЙЩЫФЁЂЯвЮхЁБЃЎЭѕРЯЪІИјГівЛзщЪ§ШУбЇЩњЙлВьЃК3ЁЂ4ЁЂ5ЃЛ5ЁЂ12ЁЂ13ЃЛ7ЁЂ24ЁЂ25ЃЛ9ЁЂ40ЁЂ41ЃЛЁЃЌбЇЩњЗЂЯжетаЉЙДЙЩ Ъ§ЕФЙДЖМЪЧЦцЪ§ЃЌЧвДг 3 Ц№ОЭУЛгаМфЖЯЙ§ЃЌгкЪЧЭѕРЯЪІЬсГівдЯТЮЪЬтШУбЇЩњНтОіЃЎ
(1)ЧыФуИљОнЩЯЪіЕФЙцТЩаДГіЯТвЛзщЙДЙЩЪ§ЃК11ЁЂ________ЁЂ________ЃЛ
(2)ШєЕквЛИіЪ§гУзжФИa(aЮЊЦцЪ§ЃЌЧвaЁн3)БэЪОЃЌФЧУДКѓСНИіЪ§гУКЌaЕФДњЪ§ЪНЗжБ№дѕУДБэЪОЃПаЁУїЗЂЯжУПзщЕкЖўИіЪ§гаетбљЕФЙцТЩ4=![]() ЃЌ12=
ЃЌ12=![]() ЃЌ24=
ЃЌ24=![]() ЁЁЃЌгкЪЧЫћКмПьБэЪОСЫЕкЖўЪ§ЮЊ
ЁЁЃЌгкЪЧЫћКмПьБэЪОСЫЕкЖўЪ§ЮЊ ![]() ЃЌдђгУКЌaЕФДњЪ§ЪНБэЪОЕкШ§ИіЪ§ЮЊ________ЃЛ
ЃЌдђгУКЌaЕФДњЪ§ЪНБэЪОЕкШ§ИіЪ§ЮЊ________ЃЛ
(3)гУЫљбЇжЊЪЖжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛДЮЪ§бЇЛюЖЏжаЃЌКкАхЩЯЛзХШчЭМЫљЪОЕФЭМаЮЃЌЛюЖЏЧАРЯЪІдкзМБИЕФЫФеХжНЦЌЩЯЗжБ№аДгаШчЯТЫФИіЕШЪНжаЕФвЛИіЕШЪНЃК ЂйAB=DCЃЛЂкЁЯABE=ЁЯDCEЃЛЂлAE=DEЃЛЂмЁЯA=ЁЯD
аЁУїЭЌбЇБеЩЯблОІДгЫФеХжНЦЌжаЫцЛњГщШЁвЛеХЃЌдйДгЪЃЯТЕФжНЦЌжаЫцЛњГщШЁСэвЛеХЃЎЧыНсКЯЭМаЮНтД№ЯТСаСНИіЮЪЬтЃК
ЃЈ1ЃЉЕБГщЕУЂйКЭЂкЪБЃЌгУЂйЃЌЂкзїЮЊЬѕМўФмХаЖЈЁїBECЪЧЕШбќШ§НЧаЮТ№ЃПЫЕЫЕФуЕФРэгЩЃЛ
ЃЈ2ЃЉЧыФугУЪїзДЭМЛђБэИёБэЪОГщШЁСНеХжНЦЌЩЯЕФЕШЪНЫљгаПЩФмГіЯжЕФНсЙћЃЈгУађКХБэЪОЃЉЃЌВЂЧѓвдвбОГщШЁЕФСНеХжНЦЌЩЯЕФЕШЪНЮЊЬѕМўЃЌЪЙЁїBECВЛФмЙЙГЩЕШбќШ§НЧаЮЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=x2+bx+cЕФЭМЯѓЙ§ЕуAЃЈЉ3ЃЌ0ЃЉКЭЕуBЃЈ1ЃЌ0ЃЉЃЌЧвгыyжсНЛгкЕуCЃЌDЕудкХзЮяЯпЩЯЧвКсзјБъЪЧЉ2ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсЩЯгавЛЖЏЕуPЃЌЧѓГіPA+PDЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌШёНЧЁїABCФкНггкЁбOЃЌЕуDдкЁбOЭтЃЈгыЕуCдкABЭЌВрЃЉЃЌЁЯABD=90ЁуЃЌЯТСаНсТлЃКЂйsinCЃОsinDЃЛЂкcosCЃОcosDЃЛЂлtanCЃОtanDЃЌе§ШЗЕФНсТлЮЊЃЈ ЃЉ 
A.ЂйЂк
B.ЂкЂл
C.ЂйЂкЂл
D.ЂйЂл
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com