Question

【题目】如图，反比例函数y= 的图象与一次函数y= x的图象交于点A、B，点B的横坐标是4．点P是第一象限内反比例函数图象上的动点，且在直线AB的上方．

（1）若点P的坐标是（1，4），直接写出k的值和△PAB的面积；
（2）设直线PA、PB与x轴分别交于点M、N，求证：△PMN是等腰三角形；
（3）设点Q是反比例函数图象上位于P、B之间的动点（与点P、B不重合），连接AQ、BQ，比较∠PAQ与∠PBQ的大小，并说明理由．

Answer 1

【答案】
（1）

解：k=4，S△PAB=15．

提示：过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，

设AP与y轴交于点C，如图1，

把x=4代入y= x，得到点B的坐标为（4，1），

把点B（4，1）代入y= ，得k=4．

解方程组 ，得到点A的坐标为（﹣4，﹣1），

则点A与点B关于原点对称，

∴OA=OB，

∴S△AOP=S△BOP，

∴S△PAB=2S△AOP．

设直线AP的解析式为y=mx+n，

把点A（﹣4，﹣1）、P（1，4）代入y=mx+n，

求得直线AP的解析式为y=x+3，

则点C的坐标（0，3），OC=3，

∴S△AOP=S△AOC+S△POC

= OCAR+ OCPS

= ×3×4+ ×3×1= ，

∴S△PAB=2S△AOP=15；

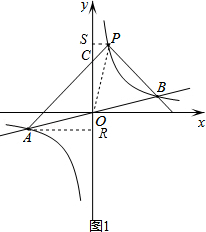
（2）

解：过点P作PH⊥x轴于H，如图2．

B（4，1），则反比例函数解析式为y= ，

设P（m， ），直线PA的方程为y=ax+b，直线PB的方程为y=px+q，

联立 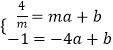，解得直线PA的方程为y= x+ ﹣1，

联立 ，解得直线PB的方程为y=﹣ x+ +1，

∴M（m﹣4，0），N（m+4，0），

∴H（m，0），

∴MH=m﹣（m﹣4）=4，NH=m+4﹣m=4，

∴MH=NH，

∴PH垂直平分MN，

∴PM=PN，

∴△PMN是等腰三角形；

（3）

解：∠PAQ=∠PBQ．

理由如下：

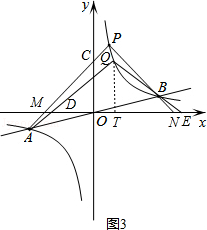
过点Q作QT⊥x轴于T，设AQ交x轴于D，QB的延长线交x轴于E，如图3．

可设点Q为（c， ），直线AQ的解析式为y=px+q，则有

，

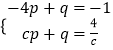解得： ，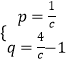

∴直线AQ的解析式为y= x+ ﹣1．

当y=0时， x+ ﹣1=0，

解得：x=c﹣4，

∴D（c﹣4，0）．

同理可得E（c+4，0），

∴DT=c﹣（c﹣4）=4，ET=c+4﹣c=4，

∴DT=ET，

∴QT垂直平分DE，

∴QD=QE，

∴∠QDE=∠QED．

∵∠MDA=∠QDE，

∴∠MDA=∠QED．

∵PM=PN，∴∠PMN=∠PNM．

∵∠PAQ=∠PMN﹣∠MDA，∠PBQ=∠NBE=∠PNM﹣∠QED，

∴∠PAQ=∠PBQ．

【解析】（1）过点A作AR⊥y轴于R，过点P作PS⊥y轴于S，连接PO，设AP与y轴交于点C，如图1，可根据条件先求出点B的坐标，然后把点B的坐标代入反比例函数的解析式，即可求出k，然后求出直线AB与反比例函数的交点A的坐标，从而得到OA=OB，由此可得S△PAB=2S△AOP ， 要求△PAB的面积，只需求△PAO的面积，只需用割补法就可解决问题；（2）过点P作PH⊥x轴于H，如图2．可用待定系数法求出直线PB的解析式，从而得到点N的坐标，同理可得到点M的坐标，进而得到MH=NH，根据垂直平分线的性质可得PM=PN，即△PMN是等腰三角形；（3）过点Q作QT⊥x轴于T，设AQ交x轴于D，QB的延长线交x轴于E，如图3．可设点Q为（c， ），运用待定系数法求出直线AQ的解析式，即可得到点D的坐标为（c﹣4，0），同理可得E（c+4，0），从而得到DT=ET，根据垂直平分线的性质可得QD=QE，则有∠QDE=∠QED．然后根据对顶角相等及三角形外角的性质，就可得到∠PAQ=∠PBQ．
【考点精析】利用确定一次函数的表达式和三角形的面积对题目进行判断即可得到答案，需要熟知确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；三角形的面积=1/2×底×高．