
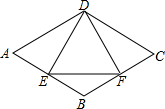
 如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:
如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先连接BD,易证得△ADE≌△BDF,然后可证得DE=DF,AE=BF,即可得△DEF是等边三角形,然后由DE⊥AB时求出DE的长,即可求出△DEF的面积.
解答 解:连接BD,如图所示:
∵四边形ABCD是菱形,
∴AD=AB,∠ADB=$\frac{1}{2}$∠ADC,AB∥CD,
∵∠A=60°,
∴∠ADC=120°,∠ADB=60°,
同理:∠DBF=60°,
即∠A=∠DBF,
∴△ABD是等边三角形,
∴AD=BD,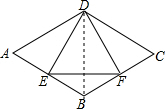
∵∠ADE+∠BDE=60°,∠BDE+∠BDF=∠EDF=60°,
∴∠ADE=∠BDF,
∵在△ADE和△BDF中,
$\left\{\begin{array}{l}{∠ADE=∠BDF}\\{AD=BD}\\{∠A=∠DBF}\end{array}\right.$,
∴△ADE≌△BDF(ASA),
∴DE=DF,AE=BF,故①正确;
∵∠EDF=60°,
∴△DEF是等边三角形,
∴②正确;
∵△ADE≌△BDF,
∴AE=BF,
同理:BE=CF,
但BE不一定等于BF.
故③错误.
∵△DEF是等边三角形,边长最短时,面积最小,
∴当DE⊥AB时,DE最短,此时E为AB的中点,BE=$\frac{1}{2}$AB=$\frac{1}{2}$AD=2,
∴DE=2$\sqrt{3}$,
∴△DEF的面积=$\frac{1}{2}$×2$\sqrt{3}$×2$\sqrt{3}$×sin60°=3$\sqrt{3}$,
∴④正确;
正确的结论有3个,故选:C.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 3 | 0 | -1 | 0 | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
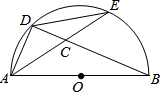 如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )
如图所示,AB是⊙O的直径,D、E是半圆上任意两点,连接AD、DE,AE与BD相交于点C,要是△ADC与△ABD相似,可以添加一个条件.下列添加的条件中错误的是( )| A. | ∠ACD=∠DAB | B. | AD=DE | C. | AD•AB=CD•BD | D. | AD2=BD•CD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com