
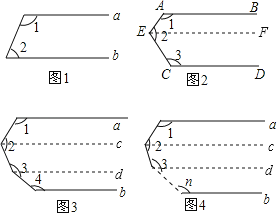
【题目】(1)如图1,a∥b,则∠1+∠2=
(2)如图2,AB∥CD,则∠1+∠2+∠3= ,并说明理由
(3)如图3,a∥b,则∠1+∠2+∠3+∠4=
(4)如图4,a∥b,根据以上结论,试探究∠1+∠2+∠3+∠4+…+∠n= (直接写出你的结论,无需说明理由)
【答案】故答案为:180°;360°;540°;(n﹣1)180°
【解析】
(1)根据两直线平行,同旁内角互补得出答案;(2)过点E作EF∥AB,根据平行线的性质得出答案;(3)过∠2、∠3的顶点作a的平行线,然后根据平行线的性质得出答案;(4)过∠2、∠3…的顶点作a的平行线,然后根据平行线的性质得出答案.
(1)∵a∥b,
∴∠1+∠2=180°;
(2)过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠1+∠AEF=180°,∠CEF+∠2=180°,
∴∠1+∠AEF+∠CEF+∠2=180°+180°,
即∠1+∠2+∠3=360°;
(3)如图,过∠2、∠3的顶点作a的平行线,
则∠1+∠2+∠3+∠4=180°×3=540°;
(4)如图,过∠2、∠3…的顶点作a的平行线,
则∠1+∠2+∠3+∠4+…+∠n=(n﹣1)180°.


科目:初中数学 来源: 题型:
【题目】如图1,二次函数y= ![]() x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.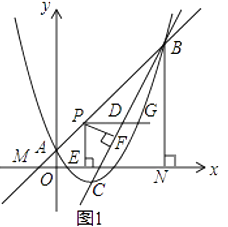
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ ![]() BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+ ![]() BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= ![]() x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K是直角三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建“美丽乡村”,某村计划购买甲、乙两种树苗共400棵,对本村道路进行绿化改造,已知甲种树苗每棵200元,乙种树苗每棵300元.
![]() 若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
若购买两种树苗的总金额为90000元,求需购买甲、乙两种树苗各多少棵?
![]() 若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
若购买甲种树苗的金额不少于购买乙种树苗的金额,则至少应购买甲种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB>BC,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于![]() EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H.则下列结论:①AG平分∠DAB,②CH=![]() DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=![]() S四边形ABCH.
S四边形ABCH.
其中正确的有( )

A. ①②③ B. ①③④ C. ②④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() (x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣
(x>0)的图象交于A(m,6),B(3,n)两点,与x轴交于点C,与y轴交于点D,下列结论:①一次函数解析式为y=﹣2x+8;②AD=BC;③kx+b﹣ ![]() <0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )
<0的解集为0<x<1或x>3;④△AOB的面积是8,其中正确结论的个数是( )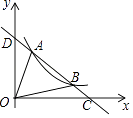
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2 ![]() ,将扇形OAB沿过点B的直线折叠,点O恰好落在
,将扇形OAB沿过点B的直线折叠,点O恰好落在 ![]() 上的点D处,折痕交OA于点C,则阴影部分的面积是 .
上的点D处,折痕交OA于点C,则阴影部分的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,过点A引射线AH,交边CD于点H(点H与点D不重合).通过翻折,使点B落在射线AH上的点G处,折痕AE交BC于E,延长EG交CD于F.
(感知)(1)如图①,当点H与点C重合时,猜想FG与FD的数量关系,并说明理由.
(探究)(2)如图②,当点H为边CD上任意一点时,(1)中结论是否仍然成立?请说明理由.
(应用)(3)在图②中,当DF=3,CE=5时,直接利用探究的结论,求AB的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com