
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,4)三点,其中a,b满足关系式a=![]() +2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
+2.若在第二象限内有一点P(m,1),使四边形ABOP的面积与三角形ABC的面积相等,则点P的坐标为( )
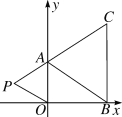
A. (-3,1) B. (-2,1) C. (-4,1) D. (-2.5,1)
【答案】A
【解析】
根据被开方数大于等于0,分母不等于0列式求出b,再求出a,从而得到A、B、C的坐标,再求出BC的长度,然后求出△ABC的面积,根据S四边形ABOP=S△AOP+S△AOB列式计算,然后列出方程求出m的值,从而得解.
由题意得,b2-9≥0且9-b2≥0,
解得,b2≥9且b2≤9,
所以,b2=9,
解得b=±3,
又∵b+3≠0,
解得b≠-3,
所以b=3,
a=2,
∴点A(0,2),B(3,0),C(3,4),
∴点B、C的横坐标都是3,
∴BC∥y轴,
∴BC=4-0=4,
△ABC的面积=![]() ×4×3=6,
×4×3=6,
∵OA=2,点P(m,![]() )在第二象限,
)在第二象限,
∴S四边形ABOP=S△AOP+S△AOB,
=![]() ×2(-m)+
×2(-m)+![]() ×2×3,
×2×3,
=-m+3,
∵四边形ABOP的面积与△ABC的面积相等,
∴-m+3=6,
解得m=-3,
所以,点P(-3,![]() ).
).
故选A.


科目:初中数学 来源: 题型:
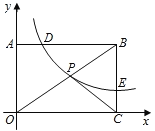
【题目】如图,已知矩形OABC中,OA=3,AB=4,双曲线y=![]() (k>0与矩形两边AB、BC分 别交于点D、E,且BD=2AD﹒
(k>0与矩形两边AB、BC分 别交于点D、E,且BD=2AD﹒
(1)求此双曲线的函数表达式及点E的坐标;
(2)若矩形OABC的对角线OB与双曲线相交于点P,连结PC,求△POC的面积﹒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 两地盛产柑桔,
两地盛产柑桔,![]() 地有柑桔200吨,
地有柑桔200吨,![]() 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知![]() 仓库可储存240吨,
仓库可储存240吨,![]() 仓库可储存260吨;从
仓库可储存260吨;从![]() 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从![]() 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从![]() 地运往
地运往![]() 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;
| C | D | 总计 |
A | x吨 | 200吨 | |
B | 300吨 | ||
总计 | 240吨 | 260吨 | 500吨 |
(2)试讨论A,B两地中,哪个运费较少;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4cm,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π) 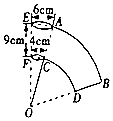
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(1,6)和点B在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. 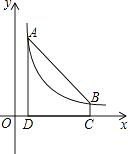
(1)求反比例函数的表达式和点B的坐标;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,以AC为直径的⊙O分别交AB,BC于点D,E,点F在AB的延长线上,2∠BCF=∠BAC. 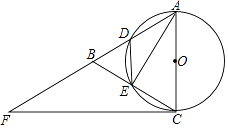
(1)求∠ADE的度数.
(2)求证:直线CF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
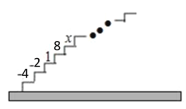
【题目】如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着﹣4,﹣2,1,8,且任意相邻四个台阶上数的和都相等.
尝试:(1)求前4个台阶上数的和是多少?
(2)求第5个台阶上的数x是多少?
应用: 求从下到上39个台阶上数的和.
发现:试用含k(k为正整数)的代数式表示出数“1”所在的台阶数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com