
【题目】已知四边形 ABCD 中, AB⊥AD,BC⊥CD,AB=BC,∠ABC=1200,∠MBN=600,将∠MBN 绕点B 旋转.当∠MBN 旋转到如图的位置,此时∠MBN 的两边分别交 AD、DC 于 E、F,且AE≠CF.延长 DC 至点 K,使 CK=AE,连接BK.
求证:(1)△ABE≌△CBK;(2)∠KBC+∠CBF=600 ;(3)CF+AE=EF.

【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】分析:(1)根据已知条件可以利用SAS证明△ABE≌△CBK;(2)由(1)可得∠KBF=∠EBF=60°,即∠KBC+∠CBF=60°;(3)再证明△EBF≌△KBF,即可得EF=CK+CF,可证AE+CF=EF.
本题解析:
证明:(1)∵AB⊥AD,BC⊥CD
∴∠BAE=∠BCK=90°
又∵AB=BC,AE=CK
∴△ABE≌△CBK
(2)由(1)可知△ABE≌△CBK
∴∠KBC=∠EBA,
又∵∠ABC=120°,∠MBN=60°
∴∠CBF+∠ABE=60°
∴∠KBC+∠CBF=60°
(3)由(1)可知△ABE≌△CBK,∴BK=BE
又∵∠KBF=∠MBN=60°,BF=BF,∴△BKF≌△BEF
∴KF=EF
又∵KF=KC+CF,CK=AE
∴CF+AE=EF


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C.
x+2与x轴交于A、B两点,与y轴交于点C.
⑴求点A,B,C的坐标;
⑵点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
⑶此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y= x2+bx+c与x轴、y轴分别相交于点A( 1,0)、B(0,3)两点,其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与x轴的另一个交点为E. 求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出P点的坐标,若不存在说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y= ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | ... | -3 | -2 | - 1 | 0 | 1 | ... |
y | ... | -6 | 0 | 4 | 6 | 6 | ... |
容易看出,(-2,0)是抛物线与x轴的一个交点,则它与x轴的另一个交点的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A(﹣3,﹣2)向上平移2个单位,再向右平移2个单位到点B,则点B的坐标为( )
A.(1,0) B.(1,﹣4) C.(﹣1,0) D.(﹣5,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
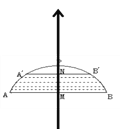
【题目】如右图所示,有一座拱桥圆弧形,它的跨度AB为60米,拱高PM为18米,当洪水泛滥到跨度只有30米时,就要采取紧急措施,若拱顶离水面只有4米,即PN=4米时,是否采取紧急措施?(![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com