
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C.
x+2与x轴交于A、B两点,与y轴交于点C.
⑴求点A,B,C的坐标;
⑵点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
⑶此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

【答案】(1)(0,2)(2)![]() (3)(﹣1,﹣1)或(﹣1,2+
(3)(﹣1,﹣1)或(﹣1,2+![]() )或(﹣1,2﹣
)或(﹣1,2﹣![]() ).
).
【解析】(1)分别令y=0,x=0,即可解决问题;(2)由图象可知AB只能为平行四边形的边,易知点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣![]() ),由此不难解决问题;(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.
),由此不难解决问题;(3)分A、C、M为顶点三种情形讨论,分别求解即可解决问题.
解:(1)令y=0得﹣![]() x2﹣
x2﹣![]() x+2=0,∴x2+2x﹣8=0,
x+2=0,∴x2+2x﹣8=0,
x=﹣4或2,∴点A坐标(2,0),点B坐标(﹣4,0),
令x=0,得y=2,∴点C坐标(0,2).
(2)由图象可知AB只能为平行四边形的边,
∵AB=EF=6,对称轴x=﹣1,
∴点E的横坐标为﹣7或5,∴点E坐标(﹣7,﹣ ![]() )或(5,﹣
)或(5,﹣![]() ),此时点F(﹣1,﹣
),此时点F(﹣1,﹣![]() )
)
∴以A,B,E,F为顶点的平行四边形的面积=6×![]() =
=![]() .
.
(3)如图所示,
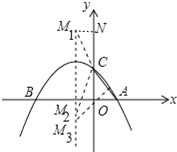
①当C为顶点时,CM1=CA,CM2=CA,作M1N⊥OC于N,
在RT△CM1N中,CN=![]() =
=![]() ,
,
∴点M1坐标(﹣1,2+![]() ),点M2坐标(﹣1,2﹣
),点M2坐标(﹣1,2﹣![]() ).
).
②当M3为顶点时,
∵直线AC解析式为y=﹣x+2,线段AC的垂直平分线为y=x,
∴点M3坐标为(﹣1,﹣1).
③当点A为顶点的等腰三角形不存在.
综上所述点M坐标为(﹣1,﹣1)或(﹣1,2+![]() )或(﹣1,2﹣
)或(﹣1,2﹣![]() ).
).
“点睛”本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识,解题的关键是熟练掌握抛物线与坐标轴交点的求法,学会分类讨论的思想,属于中考压轴题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】适合下列条件的△ABC中,直角三角形的个数为( )
①a=![]() ,b=
,b=![]() ,c=
,c=![]() ②a=6,∠A=45°; ③∠A=32°,∠B=58°;
②a=6,∠A=45°; ③∠A=32°,∠B=58°;
④a=7,b=24,c=25 ⑤a=2,b=2,c=4.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年G20杭州峰会期间,某志愿者小组有五名翻译,其中一名只会翻译法语,三名只会翻译英语,还有一名两种语言都会翻译.若从中随机挑选两名组成一组,则该组能够翻译上述两种语言的概率是多少?(请用“画树状图”的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形 ABCD 中, AB⊥AD,BC⊥CD,AB=BC,∠ABC=1200,∠MBN=600,将∠MBN 绕点B 旋转.当∠MBN 旋转到如图的位置,此时∠MBN 的两边分别交 AD、DC 于 E、F,且AE≠CF.延长 DC 至点 K,使 CK=AE,连接BK.
求证:(1)△ABE≌△CBK;(2)∠KBC+∠CBF=600 ;(3)CF+AE=EF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com