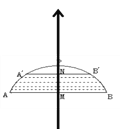
【题目】如右图所示，有一座拱桥圆弧形，它的跨度AB为60米，拱高PM为18米，当洪水泛滥到跨度只有30米时，就要采取紧急措施，若拱顶离水面只有4米，即PN=4米时，是否采取紧急措施？（）

参考答案：

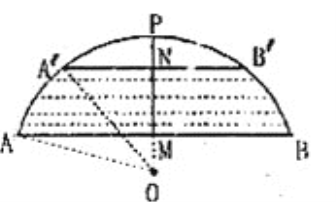
【答案】不采取紧急措施,理由见解析.

【解析】分析: 连接OA′，OA．设圆的半径是R，则ON=R-4，OM=R-18．根据垂径定理求得AM的长，在直角三角形AOM中，根据勾股定理求得R的值，在直角三角形A′ON中，根据勾股定理求得A′N的值，再根据垂径定理求得A′B′的长，从而作出判断．

本题解析:不采取紧急措施。

其理由如下：设半径OA=x ∵AB=60 PM=18,

∴AM=30 OM=,

∴在Rt△AOM中，由勾股定理，得： ,

解得：x =34 即：OA=34,OM=16

ON=(PM―PN)+OM=(18―4)+16=30

∴在Rt△AON中，由勾股定理得：

解得：AN=16 则：=32>30

所以不采取紧急措施。

关闭