
 如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么?
如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么? 分析 先由对顶角相等,得到:∠1=∠DGF,然后根据等量代换得到:∠2=∠DGF,然后根据同位角相等两直线平行,得到BD∥CE,然后根据两直线平行,同位角相等,得到∠C=∠DBA,然后根据等量代换得到:∠D=∠DBA,最后根据内错角相等两直线平行,即可得到DF与AC平行.
解答 解:DF与AC平行.
理由:∵∠1=∠DGF,∠1=∠2,
∴∠2=∠DGF,
∴BD∥CE,
∴∠C=∠DBA,
∵∠C=∠D,
∴∠D=∠DBA,
∴DF∥AC.
点评 本题考查了平行线的性质和判定的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然,题目比较好,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
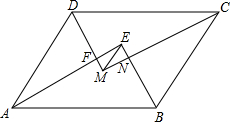 如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com