
【题目】如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C
(1)求A、B、C的坐标;
(2)过抛物线上一点F作y轴的平行线,与直线AC交于点G.若FG= ![]() AC,求点F的坐标;
AC,求点F的坐标;
(3)E(0,﹣2),连接BE.将△OBE绕平面内的某点逆时针旋转90°得到△O′B′E′,O、B、E的对应点分别为O′、B′、E′.若点B′、E′两点恰好落在抛物线上,求点B′的坐标.
【答案】
(1)
解:对于抛物线y=﹣x2﹣2x+3,
令x=0得y=3,∴C(0,3),
令y=0,则﹣x2﹣2x+3=0解得x=﹣3或1,
∴A(﹣3,0);B(1,0);C(0,3)
(2)
解:如图1中,
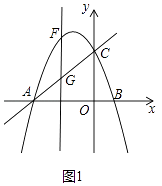
∵A(﹣3,0),C(03),
∴直线AC解析式为y=x+3,OA=OC=3,
∴AC=3 ![]() ,FG=
,FG= ![]() AC=2
AC=2
设F(m,﹣m2﹣2m+3),则G(m,m+3),
则|﹣m2﹣2m+3﹣(m+3)|=2,
解得m=﹣1或﹣2或 ![]() 或
或 ![]() ,
,
则F点的坐标为(﹣1,4)或(﹣2,3)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )
)
(3)
解:如图2中,旋转90°后,对应线段互相垂直且相等,则BE与B’E’互相垂直且相等.
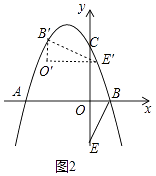
设B’(t,﹣t2﹣2t+3),则E’(t+2,﹣t2﹣2t+3﹣1)
∵E’在抛物线上,则﹣(t+2)2﹣2(t+2)+3=﹣t2﹣2t+3﹣1,
解得,t=﹣ ![]() ,则B’的坐标为(﹣
,则B’的坐标为(﹣ ![]() ,
, ![]() )
)
【解析】(1)对于抛物线分别令x=0,y=0即可解决问题.(2)先求出AC的解析式,由题意可知FG=2,设F(m,﹣m2﹣2m+3),则G(m,m+3),则有|﹣m2﹣2m+3﹣(m+3)|=2,解方程即可.(3)如图2中,旋转90°后,对应线段互相垂直且相等,则BE与B’E’互相垂直且相等.设B’(t,﹣t2﹣2t+3),则E’(t+2,﹣t2﹣2t+3﹣1).因为E’在抛物线上,则有﹣(t+2)2﹣2(t+2)+3=﹣t2﹣2t+3﹣1,解方程即可.
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品.
(1)如果随机翻1张牌,那么抽中20元奖品的概率为
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△ABE经旋转,可与△CBF重合,AE的延长线交FC于点M,以下结论正确的是( ) 
A.AM⊥FC
B.BF⊥CF
C.BE=CE
D.FM=MC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,现将一块等腰直角三角板ABC放在第二象限,斜靠在两坐标轴上,且点A(0,2),点C(﹣1,0),如图所示:抛物线y=ax2+ax﹣2经过点B.
(1)求点B的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,求所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们可以通过类比联想,引申拓展研究典型题目,可达到解一题知一类的目的,下面是一个案例,请补充完整
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)思路梳理
∵AB=AD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合.
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线.
根据 , 易证△AFG≌ , 得EF=BE+DF.
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°点E、F分别在边BC、CD上,∠EAF=45°.若∠B、∠D都不是直角,则当∠B与∠D满足等量关系时,仍有EF=BE+DF.
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°.猜想BD、DE、EC应满足的等量关系,并写出推理过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是( ) 
A.∠DAE=∠B
B.∠EAC=∠C
C.AE∥BC
D.∠DAE=∠EAC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com