
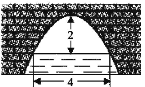
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度增加了________米.
科目:初中数学 来源: 题型:
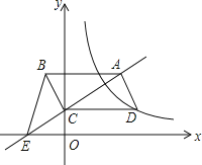
【题目】如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数![]() (x>0)的图象经过点D.已知S△BCE=1,则k=______.
(x>0)的图象经过点D.已知S△BCE=1,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
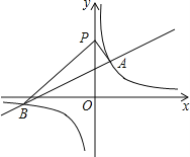
【题目】如图,一次函数y=kx+2的图象与反比例函数y=![]() 的图象交于A、B两点,其中A点坐标为(2,3).
的图象交于A、B两点,其中A点坐标为(2,3).
(1)求两个函数的表达式;
(2)点P是y轴上的一个动点,当∠APB为直角时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
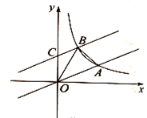
【题目】如图,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]() .
.
(1)求反比例函数的解析式;
(2)将直线![]() 向上平移后与反比例函数图象在第一象限内交于点
向上平移后与反比例函数图象在第一象限内交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间准备采取每月任务定额,超产有奖的措施提高工作效率,为制定一个恰当的生产定额,从该车间200名工人中随机抽取20人统计其某月产量如下:
每人生产零件数 | 260 | 270 | 280 | 290 | 300 | 310 | 350 | 520 |
人 数 | 1 | 1 | 5 | 4 | 3 | 4 | 1 | 1 |
(1)请应用所学的统计知识.为制定生产定额的管理者提供有用的参考数据;
(2)你认为管理者将每月每人的生产定额定为多少最合适?为什么?
(3)估计该车间全年可生产零件多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx+c的顶点为B(﹣1,3),与x轴的交点A在点(﹣3,0)和(2,0)之间,以下结论:①b2﹣4ac=0;②a+b+c>0;③2a﹣b=0;④c﹣a=3;其中正确的有( )个.
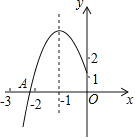
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=1,tanC=![]() ,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于![]() BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风筝又称“纸鸢”、“鸢儿”,放风筝是民间传统游戏之一,也是清明时节人们所喜爱的活动.小李打算抓住这一机遇,以每个20元的成本制作了30个风筝,再以每个40元的价格售出,很快就被一抢而空,于是小李计划加紧制作第二批风筝.
(1)预计第二批风筝的成本是每个15元,仍以原价出售,若两批风筝的总利润不低于2850元,则第二批至少应该制作多少个风筝?
(2)在实际制作过程中,小李按照(1)中风筝的最低数量进行制作,但制作风筝的成本比预期的15元多了a%(a>10),于是小李决定将售价也提高a%,附近的商户受到小李的启发,也纷纷卖起了风筝,在市场冲击下,小李实际还剩下![]() a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com