
 如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4$\sqrt{5}$,CD=8.
如图,在四边形ABCD中,AB=AD=4,∠A=60°,BC=4$\sqrt{5}$,CD=8.分析 (1)连接BD,首先证明△ABD是等边三角形,可得∠ADB=60°,DB=4,再利用勾股定理逆定理证明△BDC是直角三角形,进而可得答案;
(2)过B作BE⊥AD,利用三角形函数计算出BE长,再利用△ABD的面积加上△BDC的面积可得四边形ABCD的面积.
解答 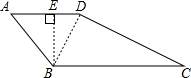 解:(1)连接BD,
解:(1)连接BD,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,DB=4,
∵42+82=(4$\sqrt{5}$)2,
∴DB2+CD2=BC2,
∴∠BDC=90°,
∴∠ADC=60°+90°=150°;
(2)过B作BE⊥AD,
∵∠A=60°,AB=4,
∴BE=AB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴四边形ABCD的面积为:$\frac{1}{2}$AD•EB+$\frac{1}{2}$DB•CD=$\frac{1}{2}$×4×$2\sqrt{3}$+$\frac{1}{2}$×4×8=4$\sqrt{3}$+16.
点评 此题主要考查了勾股定理逆定理,以及等边三角形的判定和性质,关键是掌握有一个角是60°的等腰三角形是等边三角形,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,能解释这一实际应用的数学知识是( )
如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条这样的墨线,能解释这一实际应用的数学知识是( )| A. | 两点确定一条直线 | |
| B. | 垂线段最短 | |
| C. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| D. | 两点之间,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0>|-10| | B. | -(-$\frac{1}{9}$)>-|-$\frac{1}{10}$| | C. | |-3|<|+3| | D. | -1>-0.01 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )
把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )| A. | 两地之间线段最短 | B. | 直线比曲线短 | ||
| C. | 两点之间直线最短 | D. | 两点确定一条直线 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
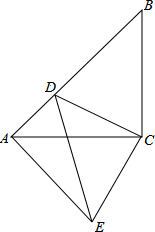 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com