
分析 (1)(2)利用不等式的性质求得不等式的解集,进一步在数轴上表示即可;
(3)求得每一个不等式的解集,求得解集的公共部分,进一步在数轴上表示即可.
解答 解:(1)1+$\frac{x}{3}$>5-$\frac{x-2}{2}$
6+2x>30-3(x-2)
2x+3x>30+6-6
5x>30
x>6
在数轴上表示如下: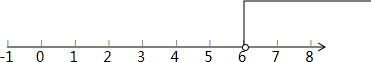
(2)3(x-2)-4(1-x)<4
3x-6-4+4x<4
7x<14
x<2
(3)$\left\{\begin{array}{l}x-3(x-2)≥4\\ \frac{1+2x}{3}>x-1\end{array}\right.$
解不等式①得:x≤1,
解不等式②得:x<4,
所以不等式组的解集为:x≤1,
在数轴上表示为:
点评 此题考查了解一元一次不等式、一元一次不等式组.在数轴上表示不等式的解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在Rt△ABC中,∠C=90°,AC=5,BC=12,若以C点为圆心、r为半径所作的圆与斜边AB只有一个公共点,则r的范围是5<r≤12或$r=\frac{60}{13}$.
在Rt△ABC中,∠C=90°,AC=5,BC=12,若以C点为圆心、r为半径所作的圆与斜边AB只有一个公共点,则r的范围是5<r≤12或$r=\frac{60}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线为二次函数y=x2-4x的图象.
如图,抛物线为二次函数y=x2-4x的图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的角平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.
如图,AB是半圆O的直径,点C是半圆上的一个动点,∠BAC的角平分线交圆弧于点D,半圆O在点D处的切线与直线AC交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A,D重合,E是直角顶点,连接EC,BE.求证:BE=CE.
如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的三角板如图放置,使三角板斜边的两个端点分别与A,D重合,E是直角顶点,连接EC,BE.求证:BE=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 班级 | 参加人数 | 中位数 | 方差 | 平均分 |
| (3)班 | 50 | 120 | 103 | 122 |
| (5)班 | 48 | 121 | 201 | 122 |
| A. | ①②③ | B. | ①② | C. | ①③ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com