
【题目】如图,已知反比例函数y1=(k1﹥0)与一次函数y2=k2x+1(k2≠0)相交于A、B两点,AC⊥x轴于点C,若△OAC的面积为1,且tan∠AOC=2.

(1)求出反比例函数与一次函数的解析式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值?
【答案】(1)、y=x+1;y=![]() ;(2)、0<x<1和x<-2.
;(2)、0<x<1和x<-2.
【解析】
试题分析:(1)、首先设OC=m,根据tan∠AOC的大小求出AC的值,然后根据三角形的面积得出m的值,从而得到点A的坐标,然后求出函数解析式;(2)、根据图象得出答案.
试题解析:(1)、在Rt△OAC中,设OC=m,∵tan∠AOC==2,∴AC=2×OC=2m,
∵S△OAC=×OC×AC=×m×2m=1, ∴m2=1,∴m=±1(负值舍去), ∴A点的坐标为(1,2),
把A点的坐标代入y1=中,得k1=2, ∴反比例函数的表达式为y1=,
把A点的坐标代入y2=k2x+1中,得k2+1=2,∴k2=1, ∴一次函数的表达式y2=x+1;
(2)、B点的坐标为(-2,-1), 当0<x<1和x<-2时,y1>y2.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
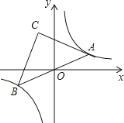
【题目】如图,点A是双曲线![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
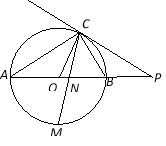
(1)求证:PC是⊙O的切线;
(2)求证:BC=AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四组线段中,能构成直角三角形的是( )
A.a=1,b=2,c=3B.a=2,b=3,c=4
C.a=2,b=4,c=5D.a=3,b=4,c=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图甲,在等边三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 度数的大小和等边三角形
度数的大小和等边三角形![]() 的边长
的边长
探究:解题思路是:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图乙,连接
,如图乙,连接![]()
(1)![]() 是_______三角形,
是_______三角形,![]() 是______三角形,
是______三角形,![]()
(2)利用![]() 可以求出
可以求出![]() 的边长为_______
的边长为_______
拓展应用:如图丙,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]()
(3)求![]() 度数的大小
度数的大小
(4)求正方形![]() 的边长
的边长
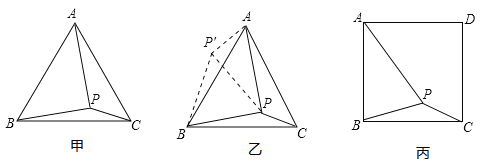
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程(x+1)2+2016=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 无实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com