
【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动,以下是根据调查结果绘制的统计图的一部分,
类别 |
|
|
|
|
|
|
类型 | 足球 | 羽毛球 | 乒乓球 | 篮球 | 排球 | 其它 |
人数 |
|
|
|
|

根据以上信息,解答下列问题:
(1)被调查学生的总人数为 人.
(2)最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %
(3)该校共有![]() 名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?
名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?
【答案】(1)50;(2)16,24;(3)180.
【解析】
(1)由喜欢羽毛球的人数10去除以它在扇形统计图中占的百分比(20%)即可求得总人数;
(2)由(1)题中求得的总人数乘以D项在扇形统计图中所占百分比可得最喜欢篮球的人数;先求出最喜欢足球的人数,再除以总人数即得最喜欢足球的学生数占被调查总人数的百分比;
(3)利用样本估计总体的方法,即可求得答案.
解:(1)10÷20%=50,所以被调查学生的总人数为50人;
故答案为50;
(2)最喜欢篮球的人数为50×32%=16,
最喜欢足球的学生数=50-10-4-16-6-2=12,
占被调查总人数的百分比为12÷50=24%;
故答案为16,24;
(3)![]() .
.
答:该校最喜欢排球的学生人数大约有180人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别 | 分数x | 频数 |
A | 40≤x<50 | 20 |
B | 50≤x<60 | 30 |
C | 60≤x<70 | 50 |
D | 70≤x<80 | m |
E | 80≤x<90 | 40 |
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,某商场推出“购物满额即可抽奖”活动.商场在抽奖箱中装有1个红球、2个黄球、3个白球、8个黑球,每个球除颜色外都相同,红球、黄球、白球分别代表一、二、三等奖,黑球代表谢谢参与.获得抽奖机会的顾客每次从箱子中摸出一个球,按相应颜色对应等级兑换奖品,每次所摸得球再放回抽奖箱,摇匀后由下一位顾客抽奖.已知小明获得1次抽奖机会.
(1)小明是否一定能中奖___________;(填是、否)
(2)求出小明抽到一等奖的概率;
(3)在这个活动中,中奖和没中奖的机会相等吗?为什么?如果不相等,可以如何改变球的个数,使中奖和没中奖的机会相等?(只写一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC、BD相交于点O,O是AC的中点,AB//DC,AC=10,BD=8.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求平行四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
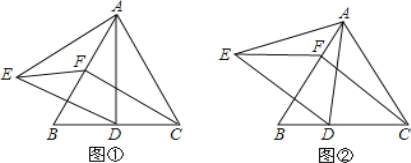
【题目】如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
(1)若点D是BC边的中点(如图①),求证:EF=CD;
(2)在(1)的条件下直接写出△AEF和△ABC的面积比;
(3)若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.
 试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒。
秒。
(1)AC=______cm;
(2)若点P恰好在∠ABC的角平分线上,求此时![]() 的值;
的值;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图,在△![]() 中,把
中,把![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得到
得到![]() ,把
,把![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,连接
,连接![]() ,当
,当![]() 时,我们称△
时,我们称△![]() 是△
是△![]() 的“旋补三角形”,△
的“旋补三角形”,△![]() 边
边![]() 上的中线
上的中线![]() 叫做
叫做![]() 的“旋补中线”,点
的“旋补中线”,点![]() 叫做“旋补中心”.
叫做“旋补中心”.
⑴ 特例感知:在如图、如图中,![]() 是
是![]() 的“旋补三角形”,
的“旋补三角形”,![]() 是
是![]() 的“旋补中线”.
的“旋补中线”.
① 如图,当![]() 为等边三角形时,
为等边三角形时,![]() 与
与![]() 的数量关系为
的数量关系为![]() =
= ![]() ;
;
② 如图,当![]() ,
,![]() 时,则
时,则![]() 长为 .
长为 .
⑵ 精确作图:如图,已知在四边形![]() 内部存在点
内部存在点![]() ,使得
,使得![]() 是
是![]() 的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点
的“旋补三角形”(点D的对应点为点A,点C的对应点为点B),请用直尺和圆规作出点![]() (要求:保留作图痕迹,不写作法和证明)
(要求:保留作图痕迹,不写作法和证明)
⑶ 猜想论证:在如图中,当△![]() 为任意三角形时,猜想
为任意三角形时,猜想![]() 与
与![]() 的数量关系,并给予证明.
的数量关系,并给予证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com