
分析 (1)根据根与系数的关系得到x1x2<0,此时方程一定有实数解,然后解不等式即可;
(2)若方程的两个根都大于1,即(x1-1)和(x2-1)同号,且和大于0,根据根与系数的关系列不等式解得;
(3)方程的两个根一个大于1,一个小于1,即x1-1和x2-1异号,利用根与系数的关系列不等式求解.
解答 解:∵x2-6x+3m-2=0,
∴△=36-4(3m-2)=44-12m,
∴x1+x2=6,x1x2=3m-2.
(1)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{3m-2>0}\end{array}\right.$,
解得:$\frac{2}{3}$<m<$\frac{11}{3}$;
(2)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{{1}^{2}-6×1+3m-2>0}\end{array}\right.$,
解得:$\frac{7}{3}$<m<$\frac{11}{3}$;
(3)根据题意得:$\left\{\begin{array}{l}{44-12m>0}\\{({x}_{1}-1)({x}_{2}-1)=3m-7<0}\end{array}\right.$,
解得:m<$\frac{7}{3}$.
点评 本题考查的知识点是一元二次方程根与系数的关系以及根的判别式等知识,其中由韦达定理(一元二次方程根与系数的关系)结合已知,构造出关k的不等式组是解答本题的关键.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:2016-2017学年重庆市校七年级下学期第一阶段考试数学试卷(解析版) 题型:单选题
如图,直线AB、CD、EF相交于点O,其中AB⊥CD,∠1:∠2=3:6,则∠EOD=( )
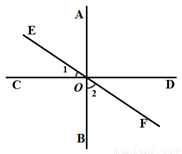
A. 120° B. 130° C. 60° D. 150°
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:判断题
小强从自己家的阳台上,看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,小强家与这栋楼的水平距离为42m,这栋楼有多高?
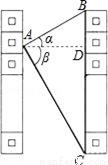
查看答案和解析>>
科目:初中数学 来源:2017届山东省中考模拟数学试卷(解析版) 题型:单选题
下列计算正确的是( )
A. a3+a2=a5 B. a3﹣a2=a C. a3•a2=a6 D. a3÷a2=a
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
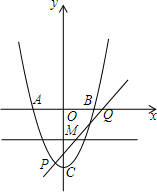 如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.
如图,抛物线y=x2-4分别交x轴于A、B,交y轴于C,P为第三象限的抛物线上一点,过P点的直线y=kx-3交直线y=-2于点M,交抛物线于另一点Q,若P、Q两点关于M成中心对称,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
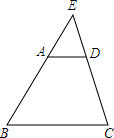 如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.
如图,在梯形ABCD中,AD∥BC,延长两腰交于点E,若AD=2,BC=6,AB=4,则$\frac{ED}{EC}$=$\frac{1}{3}$,$\frac{DE}{DC}$=$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com