
分析 根据反比例函数的定义进行解答.
解答 解:①x(y+2)=1是y+2关于x的反比例函数,故①错误;
②y=$\frac{1}{x+1}$是y关于x+1的反比例函数,故②错误;
③y=$\frac{1}{{x}^{2}}$是y关于x2的反比例函数,故③错误;
④y=-$\frac{1}{2x}$是y关于x的反比例函数,故④正确;
⑤y=-$\frac{x}{2}$是y关于x的正比例函数,故⑤错误;
⑥y=$\frac{1}{2x}$是y关于x的反比例函数,故⑥正确;
故答案是:④⑥.
点评 本题考查了反比例函数的定义.反比例函数解析式的一般形式$y=\frac{k}{x}$(k≠0),也可转化为y=kx-1(k≠0)的形式,特别注意不要忽略k≠0这个条件.


科目:初中数学 来源: 题型:解答题
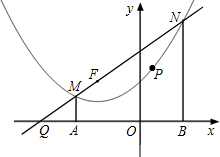 如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{8}}$和$\sqrt{18}$ | B. | $\sqrt{63}$和$\sqrt{\frac{25}{28}}$ | C. | $\sqrt{48}$和$\sqrt{4.8}$ | D. | $\sqrt{0.125}$和$\sqrt{128}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
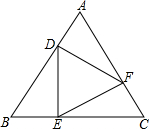 如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.
如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个角互余的三角形一定是直角三角形 | |
| B. | 直角三角形中,若一直角边等于斜边的一半,则这条直角边所对的角为30° | |
| C. | 直角三角形斜边上的中线等于斜边的一半 | |
| D. | △ABC中,若∠A:∠B:∠C=1:3:5,则这个三角形为直角三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
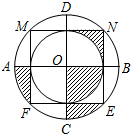 如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.
如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com