
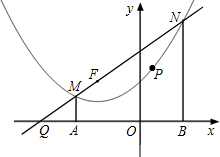
 ��ͼ������F��-2��2����ֱ��l��������y=$\frac{1}{4}$x2+x+2���ڵ�M��N���㣨��M�ڵ�N����ߣ���MA��x���ڵ�A��NB��x���ڵ�B��
��ͼ������F��-2��2����ֱ��l��������y=$\frac{1}{4}$x2+x+2���ڵ�M��N���㣨��M�ڵ�N����ߣ���MA��x���ڵ�A��NB��x���ڵ�B������ ��1��ֱ�Ӹ��������ߵĶ������꼴�ɵó����ۣ�
��2�����N�����꣬���ô���ϵ�������ɵó�ֱ��l�Ľ���ʽ�����P������ΪP��m��$\frac{1}{4}$m2+m+2��������P��PE��y�ᣬ��ֱ��l�ڵ�E�����E������ΪE��m��$\frac{3}{4}$m+$\frac{7}{2}$�������ɶ��κ��������ʼ��ɵó����ۣ�
��3����NF=NB����1=��2���ٸ��ݡ�AFB=90�㣬NB��x���ڵ�B�ó���3=��4���ʡ�FQA�ס�BQF�������������εĶ�Ӧ�߳ɱ������QF�ij�����FH��x���ڵ�H�����ô���ϵ�������ֱ��l�Ľ���ʽ�������ɵó����ۣ�
��� �⣺��1���������ߵĽ���ʽΪy=$\frac{1}{4}$x2+x+2=$\frac{1}{4}$��x+2��2+1��
���䶥������Ϊ��-2��1����
�ʴ�Ϊ��-2��1����
��2���ߵ�N�ĺ�����Ϊ2��
��y=$\frac{1}{4}$��4+2+2=5��
��N��2��5����
��F��-2��2����
����ֱ��l�Ľ���ʽΪy=kx+b��k��0����
��$\left\{\begin{array}{l}2k+b=5\\-2k+b=2\end{array}\right.$�����$\left\{\begin{array}{l}k=\frac{3}{4}\\ b=\frac{7}{2}\end{array}\right.$��
��ֱ��l�Ľ���ʽΪΪ��y=$\frac{3}{4}$x+$\frac{7}{2}$��
���P������ΪP��m��$\frac{1}{4}$m2+m+2��������P��PE��y�ᣬ��ֱ��l�ڵ�E�����E������ΪE��m��$\frac{3}{4}$m+$\frac{7}{2}$����
��PE=yE-yP=��$\frac{3}{4}$m+$\frac{7}{2}$��-��$\frac{1}{4}$m2+m+2��=-$\frac{1}{4}$m2-$\frac{1}{4}$m+$\frac{3}{2}$��
�ߵ�PE���ʱ��PMN��������PE=-$\frac{1}{4}$m2-$\frac{1}{4}$m+$\frac{3}{2}$=-$\frac{1}{4}$��m+$\frac{1}{2}$��2+$\frac{25}{16}$��
�൱m=-$\frac{1}{2}$ʱ��PE�����ʱP������ΪP��-$\frac{1}{2}$��$\frac{25}{16}$����
�ʴ�Ϊ��y=$\frac{3}{4}$x+$\frac{7}{2}$��
��3����NF=NB��
���1=��2��
�֡ߡ�AFB=90�㣬NB��x���ڵ�B��
���3+��1=90�㣬��4+��2=90��
���3=��4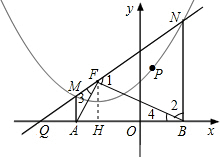
�֡ߡ�FQA=��BQF��
���FQA�ס�BQF��
��$\frac{QF}{QA}$=$\frac{QB}{QF}$��
��QF2=QB•QA=20��
��QF=2$\sqrt{5}$��
��FH��x���ڵ�H����HQ2=$\sqrt{{QF}^{2}-{FH}^{2}}$=$\sqrt{20-4}$=4��
��Q��-6��0����
��ֱ��l�Ľ���ʽΪy=kx+b��k��0����
��F��-2��2����Q��-6��0���������ʽ��$\left\{\begin{array}{l}-2k+b=2\\-6k+b=0\end{array}\right.$�����$\left\{\begin{array}{l}k=\frac{1}{2}\\ b=3\end{array}\right.$��
��y=$\frac{1}{2}$x+3��
��$\frac{1}{2}$x+3=$\frac{1}{4}$x2+x+2��
���x1=-1-$\sqrt{5}$��x2=-1+$\sqrt{5}$����ȥ��
��M��-1-$\sqrt{5}$��$\frac{5-\sqrt{5}}{2}$����
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����κ�����һ�κ����Ľ������⡢���ɶ������ô���ϵ������һ�κ����Ľ���ʽ��֪ʶ���ڽ��3��ʱҪע�����������ߣ������ֱ�������Σ����ù��ɶ�����⣮


 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д� �����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д�
�����̸�Ӯ����ٸ�Ч�����ܸ�ϰ���ϿƼ�������ϵ�д� �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
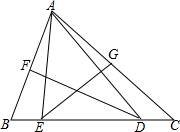 ��ͼ���ڡ�ABC�У���C=40�㣬��B=68�㣬AB��AC�Ĵ�ֱƽ���߷ֱ�BC��D��E�����EAD�Ķ�����
��ͼ���ڡ�ABC�У���C=40�㣬��B=68�㣬AB��AC�Ĵ�ֱƽ���߷ֱ�BC��D��E�����EAD�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
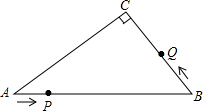 ��ͼ����Rt��ABC�У���C=90�㣬AB=10cm��AC��BC=4��3����P�ӵ�A������AB�������B�˶����ٶ�Ϊ1cm/s��ͬʱ��Q�ӵ�B������B��C��A�������A�˶����ٶ�Ϊ2cm/s����һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶���
��ͼ����Rt��ABC�У���C=90�㣬AB=10cm��AC��BC=4��3����P�ӵ�A������AB�������B�˶����ٶ�Ϊ1cm/s��ͬʱ��Q�ӵ�B������B��C��A�������A�˶����ٶ�Ϊ2cm/s����һ���˶��㵽���յ�ʱ����һ���˶���Ҳ��ֹ֮ͣ�˶����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
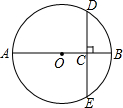 ��ͼ����O��ֱ��AB=8����DE����OB���е�C��DE��OB������DE�ij�Ϊ��������
��ͼ����O��ֱ��AB=8����DE����OB���е�C��DE��OB������DE�ij�Ϊ��������| A�� | 3$\sqrt{2}$ | B�� | 2$\sqrt{3}$ | C�� | 4$\sqrt{3}$ | D�� | 6$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��-1 | B�� | m��0 | C�� | m��1 | D�� | m��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com