
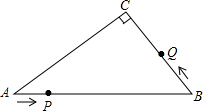
 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.分析 (1)由在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,设AC=4y,BC=3y,由勾股定理即可求得AC、BC的长;
(2)若△PBQ与△ABC相似,①如图1,∠PQB=∠C=90°,得到$\frac{PB}{AB}=\frac{BQ}{BC}$,解$\frac{10-t}{10}=\frac{2t}{6}$,得到t=$\frac{30}{13}$,②如图2,∠QPB=∠C=90°,由$\frac{PB}{BC}=\frac{BQ}{AB}$,得到方程$\frac{10-t}{6}=\frac{2t}{10}$,t=$\frac{50}{11}$>3,于是得到结论;
(3)由PQ⊥AB,可得△APQ∽△ACB,由相似三角形的对应边成比例,求得△PBQ各边的长,根据相似三角形的判定,即可得以点B、P、Q为顶点的三角形与△ABC不相似.
解答 解:(1)设AC=4x,BC=3x,在Rt△ABC中,AC2+BC2=AB2,
即:(4x)2+(3x)2=102,
解得:x=2,
∴AC=8cm,BC=6cm;
(2)若△PBQ与△ABC相似,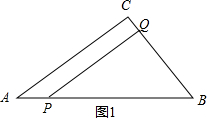 由已知条件得:AP=t,BQ=2t,
由已知条件得:AP=t,BQ=2t,
∴PB=10-t,
①如图1,∠PQB=∠C=90°,
∴$\frac{PB}{AB}=\frac{BQ}{BC}$,即$\frac{10-t}{10}=\frac{2t}{6}$,
解得:t=$\frac{30}{13}$;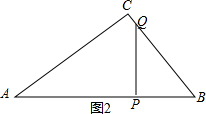 ②如图2,∠QPB=∠C=90°,
②如图2,∠QPB=∠C=90°,
∴$\frac{PB}{BC}=\frac{BQ}{AB}$,即$\frac{10-t}{6}=\frac{2t}{10}$,
解得:t=$\frac{50}{11}$>3.
综上所述:当t=$\frac{30}{13}$时,△PBQ与△ABC相似;
(3)如图3,当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为顶点的三角形与△ABC不相似.理由如下:
∵AP=x,
∴AQ=14-2x,
∵PQ⊥AB,
∴△APQ∽△ACB,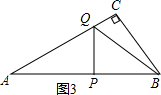
∴$\frac{AP}{AC}$=$\frac{AQ}{AB}=\frac{PQ}{BC}$,
即:$\frac{x}{8}=\frac{14-2x}{10}=\frac{PQ}{6}$,
解得:x=$\frac{56}{13}$,PQ=$\frac{42}{13}$,
∴PB=10-x=$\frac{74}{13}$,
∴$\frac{PQ}{PB}$=$\frac{\frac{42}{13}}{\frac{74}{13}}$=$\frac{21}{37}$≠$\frac{BC}{AC}$,
∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为顶点的三角形与△ABC不相似.
点评 本题考查了相似三角形的判定与性质,勾股定理,以及最短距离问题.此题综合性很强,难度较大,解题的关键是方程思想与数形结合思想的应用


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
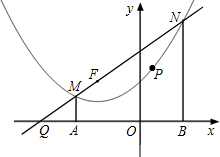 如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
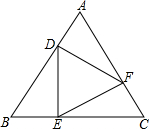 如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.
如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com