
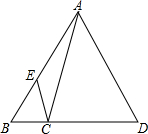
 如图.已知CD=2BC,AE=2BE,则三角形BEC的面积和三角形ABD的面积比是$\frac{1}{9}$.
如图.已知CD=2BC,AE=2BE,则三角形BEC的面积和三角形ABD的面积比是$\frac{1}{9}$. 分析 根据CD=2BC,于是得到BC=$\frac{1}{3}$BD,推出S△ABC=$\frac{1}{3}$S△ABD,由AE=2BE,得到AB=3BE,推出S△BCE=$\frac{1}{3}$S△ABC,于是求得S△BEC=$\frac{1}{3}×\frac{1}{3}$S△ABD=$\frac{1}{9}$S△ABD,即可得到结论.
解答 解:∵CD=2BC,∴BC=$\frac{1}{3}$BD,
∴S△ABC=$\frac{1}{3}$S△ABD,
∵AE=2BE,∴AB=3BE,
∴S△BCE=$\frac{1}{3}$S△ABC,
∴S△BEC=$\frac{1}{3}×\frac{1}{3}$S△ABD=$\frac{1}{9}$S△ABD,
∴$\frac{{S}_{△BCE}}{{S}_{△ABD}}$=$\frac{1}{9}$.
故答案为:$\frac{1}{9}$.
点评 本题考查了三角形的面积,熟练掌握等高三角形的面积的比等于底的比是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
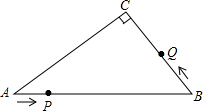 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.
如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.5×107 | B. | 9.5×108 | C. | 9.5×109 | D. | 9.5×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com