
分析 (1)利用描点法可画出这两个函数的图象,分别根据图象可得对称轴及顶点坐标.
(2)利用描点法可画出这两个函数的图象,分别根据图象可得对称轴及顶点坐标.
(3)利用描点法可画出这两个函数的图象,分别根据图象可得对称轴及顶点坐标.
解答 解:(1)两个函数的图象如图所示: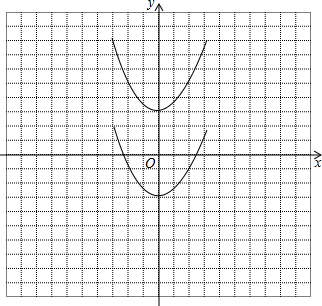
由图象可知它们的对称轴为y轴,函数y=$\frac{1}{2}$x2+3顶点坐标为(0,3),函数y=$\frac{1}{2}$x2-3的顶点坐标为(0,-3);
(2)两个函数的图象如图所示: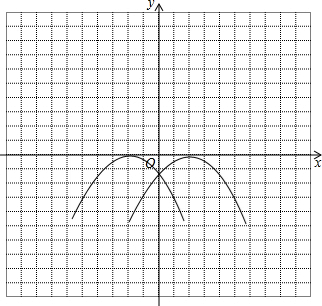
由图象可知函数y=-$\frac{1}{3}$(x+2)2的对称轴x=-2,顶点坐标为(-2,0),函数y=-$\frac{1}{3}$(x-2)2的对称轴x=2,顶点坐标为(2,0);
(3)两个函数的图象如图所示: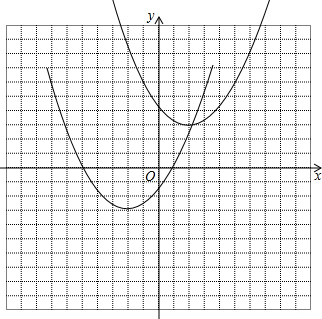
由图象可知函数y=$\frac{1}{3}$(x+2)2-3的对称轴x=-2,顶点坐标为(-2,-3),函数y=$\frac{1}{3}$(x-2)2+3的对称轴x=2,顶点坐标为(2,3).
点评 本题主要考查函数图象的画法及二次函数的图象的性质,掌握基本的描点法作函数图象是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
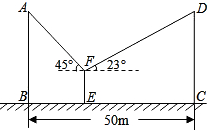 已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com