
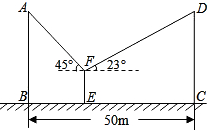
 已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43) 分析 过点F作AB、CD的垂线,垂足为点G、H,设AG=DH=x,由$\frac{AG}{tan45°}$+$\frac{AG}{tan23°}$=BC,解得AG的值,则根据AB=AG+FE即可求出电线杆的高度.
解答 解:过点F作AB、CD的垂线,垂足为点G、H.
设AG=xm,则有DH=xm.
$\frac{AG}{tan45°}$+$\frac{AG}{tan23°}$=BC,
∴tan23°=$\frac{x}{50-x}$,
解得:x≈15.0,
∴AB=x+1.5=16.5.
答:电线杆的高度约为16.5m.
故答案为:16.5.
点评 本题考查了解直角三角形的应用--仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
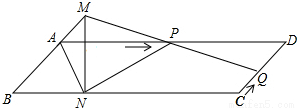 已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
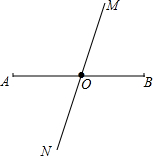 如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小.
如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9.5×107 | B. | 9.5×108 | C. | 9.5×109 | D. | 9.5×1010 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com