
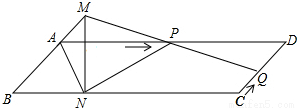
 已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)
已知:如图,?ABCD中,AD=3cm,CD=1cm,∠B=45°,点P从点A出发,沿AD方向匀速运动,速度为3cm/s;点Q从点C出发,沿CD方向匀速运动,速度为1cm/s,连接并延长QP交BA的延长线于点M,过M作MN⊥BC,垂足是N,设运动时间为t(s)(0<t<1)分析 (1)首先根据BM∥CD,可得$\frac{AM}{DQ}=\frac{AP}{DP}$,据此求出AM的值是多少;然后判断出△BMN是等腰直角三角形,即可求出MN的值是多少.
(2)首先判断出MN⊥AD,然后根据四边形ANPM的面积为$\frac{9\sqrt{2}}{16}$cm2,可得$\frac{1}{2}$×$\frac{\sqrt{2}}{2}(t+1)$×3t=$\frac{9\sqrt{2}}{16}$,据此求出t的值是多少即可.
(3)首先判断出AM=QD,然后根据AM∥QD,推得四边形MAQD是平行四边形即可.
(4)存在某一时刻t,使AO:OC=$\sqrt{2}$:1.根据AD∥BC,可得$\frac{AP}{CN}=\frac{AO}{OC}$,所以$\frac{3t}{3-\frac{\sqrt{2}}{2}(t+1)}=\sqrt{2}$,据此求出t的值是多少即可.
解答 解:(1)∵BM∥CD,
∴$\frac{AM}{DQ}=\frac{AP}{DP}$,
∴$\frac{AM}{1-t}=\frac{3t}{3-3t}$,
解得AM=t.
∵MN⊥BC,
∴∠MNB=90°,
又∵∠B=45°,
∴MN=$\frac{\sqrt{2}}{2}$BM=$\frac{\sqrt{2}}{2}(t+1)$.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,
∵MN⊥BC,
∴MN⊥AD,
∵四边形ANPM的面积为$\frac{9\sqrt{2}}{16}$cm2,
∴$\frac{1}{2}$×$\frac{\sqrt{2}}{2}(t+1)$×3t=$\frac{9\sqrt{2}}{16}$,
整理,可得4t2+4t-3=0,
解得t=$\frac{1}{2}$或t=-$\frac{3}{2}$(舍去),
∴四边形ANPM的面积为$\frac{9\sqrt{2}}{16}$cm2,t的值是$\frac{1}{2}$.
(3)如图1,连接MD、AQ,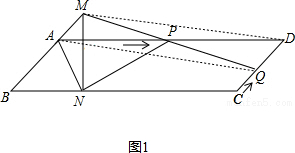 ,
,
由(2),可得t=$\frac{1}{2}$,
∴AM=$\frac{1}{2}$,QD=CD-CQ=1-$\frac{1}{2}$=$\frac{1}{2}$,
∴AM=QD,
又∵AM∥QD,
∴四边形MAQD是平行四边形.
(4)存在某一时刻t,使AO:OC=$\sqrt{2}$:1,理由如下:
如图2,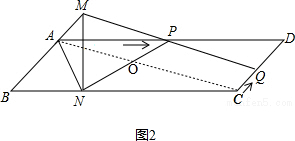
∵∠MNB=90°,∠B=45°,
∴△BMN是等腰直角三角形,
∴BN=MN=$\frac{\sqrt{2}}{2}$(t+1),
∵AD∥BC,
∴$\frac{AP}{CN}=\frac{AO}{OC}$,
∴$\frac{3t}{3-\frac{\sqrt{2}}{2}(t+1)}=\sqrt{2}$,
解得t=$\frac{3\sqrt{2}-1}{4}$,
∴存在t=$\frac{3\sqrt{2}-1}{4}$时,AO:OC=$\sqrt{2}$:1.
故答案为:t、$\frac{\sqrt{2}}{2}(t+1)$.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了平行四边形的判定和性质的应用,以及三角形的面积的求法,要熟练掌握.
(3)此题还考查了平行线的性质和应用,要熟练掌握,解答此题的关键是要明确:①定理1:两条平行线被第三条直线所截,同位角相等.简单说成:两直线平行,同位角相等.②定理2:两条平行线被地三条直线所截,同旁内角互补.简单说成:两直线平行,同旁内角互补.③定理3:两条平行线被第三条直线所截,内错角相等.简单说成:两直线平行,内错角相等.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
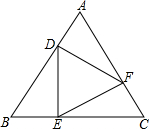 如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.
如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
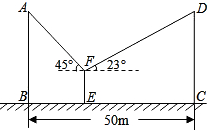 已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | -1或1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com