
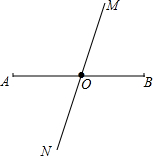
 如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小.
如图,直线MN和线段AB相交于点O,且O为AB中点,这射线OM上取一点P,画出线段PA和PB,再比较点P到点A和点B的距离的大小,在射线ON上取一点Q,画出线段QA和QB,再比较点Q到点A和点B的距离的大小. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
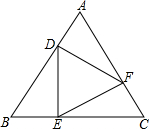 如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.
如图,在等边△ABC中,D、E、F三点分别在AB,BC,AC上,DE⊥BC于E,EF⊥AC于F,FD⊥AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
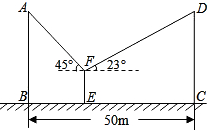 已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)
已知相邻的两根电线杆AB与CD高度相同,且相距BC=50m.小王为测量电线杆的高度,在两根电线杆之间某一处E架起测角仪,如图所示,分别测得两根电线杆顶端的仰角为45°、23°,已知测角仪EF高1.5m,则电线杆的高度约为16.5m.(精确到0.1m,参考数据:sin23°≈0.39,cos23°≈0.92,tan23°≈0.43)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com