
| A. | m≥-1 | B. | m>0 | C. | m≥1 | D. | m≥0 |
科目:初中数学 来源: 题型:解答题
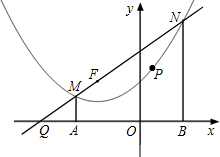 如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
如图,过点F(-2,2)的直线l与抛物线y=$\frac{1}{4}$x2+x+2交于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
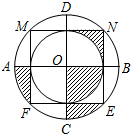 如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.
如图,边长为2的正方形MNEF的四个顶点在大圆O上,小圆O与正方形各边都相切,AB与CD是大圆O的直径,AB⊥CD,CD⊥MN,则图中阴影部分的面积是$\frac{1}{2}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
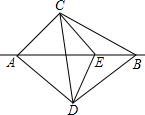 如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.
如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 服饰 | 原价(元) |
| 外套 | 299 |
| 衬衫 | 199 |
| 裤子 | 199 |
| A. | 0.8×199x+0.6×299(200+x)=33860 | B. | 0.8×199x+0.6×299(200-x)=33860 | ||
| C. | 0.6×299x+0.8×199(200+x)=33860 | D. | 0.6×299x+08×199(200-x)=33860 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com