
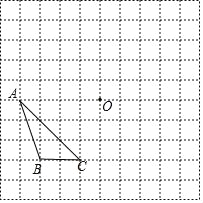
【题目】如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A,B,C及点O均在格点上请按要求完成以下操作或运算:
(1)将△ABC绕点O旋转90°,得到△A1B1C1;
(2)求点B旋转到点B1的路径长(结果保留π).
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象如图所示,给出下列结论:①b2>4ac; ②abc<0;③a<b; ④b+c>3a;⑤方程ax2+bx+c=0的两根之和的一半大于﹣1.其中,正确的结论有( )
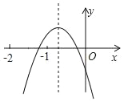
A. ①②③⑤B. .①②④⑤C. ①②④D. .①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
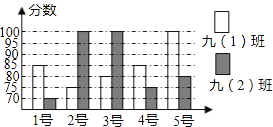
【题目】我区某中学开展“社会主义核心价值观”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.根据图中数据解决下列问题:
(1)九(1)班复赛成绩的中位数是 分,九(2)班复赛成绩的众数是 分;
(2)小明同学已经算出了九(1)班复赛的平均成绩![]() =85分;方差S2=
=85分;方差S2=![]() [(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
[(85﹣85)2+(75﹣85)2+(80﹣85)2+(85﹣85)2+(100﹣85)2]=70(分2),请你求出九(2)班复赛的平均成绩x2和方差S22;
(3)根据(2)中计算结果,分析哪个班级的复赛成绩较好?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一年一度的“春节”即将到来,某超市购进一批价格为每千克3元的桔子,根据市场预测,该种桔子每千克售价4元时,每天能售出500千克,并且售价每上涨0.1元,其销售量将减少10千克,物价部门规定,该种桔子的售价不能超过进价的200%,请你利用所学知识帮助超市给这种桔子定价,使得超市每天销售这种桔子的利润为800元.
查看答案和解析>>
科目:初中数学 来源: 题型:
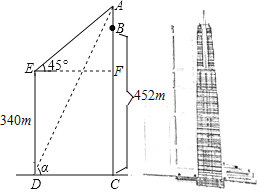
【题目】如图,长沙九龙仓国际金融中心主楼BC高达452m,是目前湖南省第一高楼,和它处于同一水平面上的第二高楼DE高340m,为了测量高楼BC上发射塔AB的高度,在楼DE底端D点测得A的仰角为α,在顶端E点测得A的仰角∠AEF=45°,
(1)若设AB为x米,请用含x的代数式表示AF的长.
(2)求出发射塔AB的高度.(cosα≈![]() ,sinα≈
,sinα≈![]() ,tanα≈
,tanα≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x﹣3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=﹣x2+mx+n与x轴的另一个交点为A,顶点为P.
(1)求3m+n的值;
(2)在该抛物线的对称轴上是否存在点Q,使以C,P,Q为顶点的三角形为等腰三角形?若存在,求出有符合条件的点Q的坐标;若不存在,请说明理由.
(3)将该抛物线在x轴上方的部分沿x轴向下翻折,图象的其余部分保持不变,翻折后的图象与原图象x轴下方的部分组成一个“M“形状的新图象,若直线y=x+b与该“M”形状的图象部分恰好有三个公共点,求b的值.
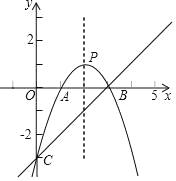
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x=﹣1的抛物线y=x2+bx+c与x轴相交于A、B两点,其中点A的坐标为(﹣3,0).
(1)求点B的坐标;
(2)求二次函数的解析式;
(3)已知C为抛物线与y轴的交点,设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抛掷硬币的试验中,下列结论正确的是![]()
![]()
A. 经过大量重复的抛掷硬币试验,可发现“正面向上”的频率越来越稳定
B. 抛掷10000次硬币与抛掷12000次硬币“正面向上”的频率相同
C. 抛掷50000次硬币,可得“正面向上”的频率为![]()
D. 若抛掷2000次硬币“正面向上”的频率是![]() ,则“正面向下”的频率也为
,则“正面向下”的频率也为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛预赛.各参赛选手的成绩如图:
九(1)班:88,91,92,93,93,93,94,98,98,100
九(2)班:89,93,93,93,95,96,96,98,98,99
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
九(1)班 | 100 | m | 93 | 93 | 12 |
九(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)直接写出表中m、n的值;
(2)依据数据分析表,有人说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有人说(2)班的成绩要好,请给出两条支持九(2)班成绩好的理由;
(3)若从两班的参赛选手中选四名同学参加决赛,其中两个班的第一名直接进入决赛,另外两个名额在四个“98分”的学生中任选二个,试求另外两个决赛名额落在同一个班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com