练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知点A（m，m＋1），B（m＋3，m－1）是反比例函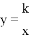数与一次函数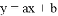的交点．

    （1）求反比例函数与一次函数的解析式；

    （2）请直接写出当反比例函数的函数值不大于一次函数的函数值时，自变量x的取值范围．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017届江苏省扬州市九年级下学期第一次月考数学试卷（解析版） 题型：填空题

    若3a2﹣a﹣3=0，则2017+2a﹣6a2=　__________．

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省九年级上学期第二次月考数学试卷（解析版） 题型：判断题

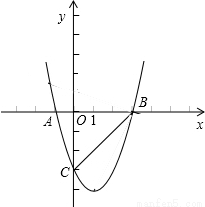
    已知如图，抛物线y＝x2＋mx＋n与x轴交于A、B两点，与y轴交于点C．若A(－1，0)，且OC＝3OA

    (1) 求抛物线的解析式

    (2) 若M点为抛物线上第四象限内一动点，顺次连接AC、CM、MB，求四边形MBAC面积的最大值

    (3) 将直线BC沿x轴翻折交y轴于N点，过B点的直线l交y轴、抛物线分别于D、E，且D在N的上方．若∠NBD＝∠DCA，试求E点的坐标

    查看答案和解析>>

    科目：初中数学 来源：2017届湖北省九年级上学期第二次月考数学试卷（解析版） 题型：单选题

    从正方形铁片上截取2 cm宽的一个矩形，剩余矩形的面积为80 cm2，则圆正方形的面积为（ ）

    A. 100 cm2 B. 121 cm2 C. 144 cm2 D. 169 cm2

    查看答案和解析>>

    科目：初中数学 来源：2017届福建省九年级上学期第二次阶段性测试数学试卷（解析版） 题型：判断题

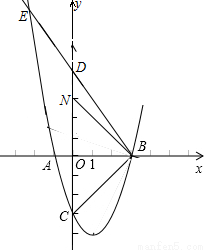
    如图，在平面直角坐标系中，直线l1过点B（0，－1），且平行于x轴，直线l2过点C（0，－2），交直线l1于点D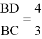，，点A与点B关于x轴对称，点P为抛物线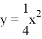上一动点，PQ⊥l1于点Q．

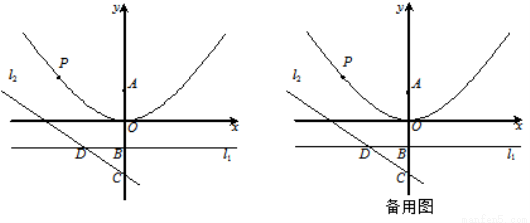
    （1）求直线l2的函数关系式；

    （2）连接PA，AQ，OD，是否存在点P，使△PAQ与△OCD相似，若存在，求出点P坐标；若不存在，请说明理由；

    （3）当点P到直线l1与直线l2的距离之和最短时，求出点P坐标及最短距离．

    查看答案和解析>>

    科目：初中数学 来源：2017届福建省九年级上学期第二次阶段性测试数学试卷（解析版） 题型：填空题

    已知实数、满足，则代数式的最小值等于______．

    查看答案和解析>>

    科目：初中数学 来源：2017届福建省九年级上学期第二次阶段性测试数学试卷（解析版） 题型：填空题

    已知点P（1，﹣3），则点P关于原点对称的点的坐标是__．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省七年级下学期第一次月考（3月）数学试卷（解析版） 题型：解答题

    计算：

    ①（﹣2x）（4x2﹣2x+1） ②（6a3﹣4a2+2a）÷2a

    ③a4 +(a2)4 -(a2)2 ④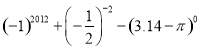

    ⑤（2a+b）2 ⑥ (3x+7y)(3x-7y)

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省八年级下学期第一次月考（3月）数学试卷（解析版） 题型：判断题

    先阅读理解下面的例题，再按要求解答下列问题：

    例题：解一元二次不等式x2﹣4＞0

    【解析】
    ∵x2﹣4=（x+2）（x﹣2）

    ∴x2﹣4＞0可化为

    （x+2）（x﹣2）＞0

    由有理数的乘法法则“两数相乘，同号得正”，得

    ①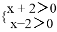 ②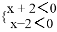

    解不等式组①，得x＞2，

    解不等式组②，得x＜﹣2，

    ∴（x+2）（x﹣2）＞0的解集为x＞2或x＜﹣2，

    即一元二次不等式x2﹣4＞0的解集为x＞2或x＜﹣2．

    解答下列问题：

    （1）一元二次不等式x2﹣25＞0的解集为　 　 ；

    （2）分式不等式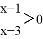的解集为　 　 ；

    （3）解一元二次不等式2x2﹣3x＜0．

    查看答案和解析>>

    同步练习册答案